Blog
Articles about computational science and data science, neuroscience, and open source solutions. Personal stories are filed under Weekend Stories. Browse all topics here. All posts are CC BY-NC-SA licensed unless otherwise stated. Feel free to share, remix, and adapt the content as long as you give appropriate credit and distribute your contributions under the same license.
tags · RSS · Mastodon · simple view · page 15/16
The Weierstrass function and the beauty of fractals
Fractals are captivating mathematical objects that exhibit intricate patterns and self-similarity at various scales. In this post, we explore the elegance and significance of the Weierstrass function, its relation to fractals and fractal geometry, and discuss other notable fractals. Through this journey, we will discover the fascinating world of fractal geometry and its beautiful and profound impact.
Running a personal website with Jekyll
I have redesigned my website and moved it to a new host as well: I’m running it as personal Jekyll website hosted on GitHub now.
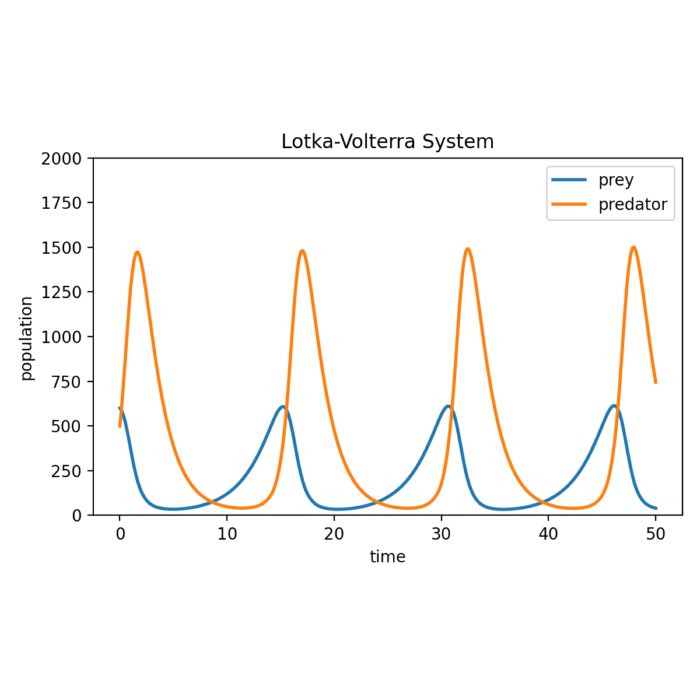
The Lotka-Volterra equations: Modeling predator-prey dynamics
The Lotka-Volterra system, also known as the predator-prey equations, is a mathematical model that describes the interaction between two species: predators and their prey. The system captures the dynamic relationship between the population sizes of predators and prey over time, highlighting the intricate balance between them. In this post we explore this system and calculate its numerical solution using numerical integration Python.
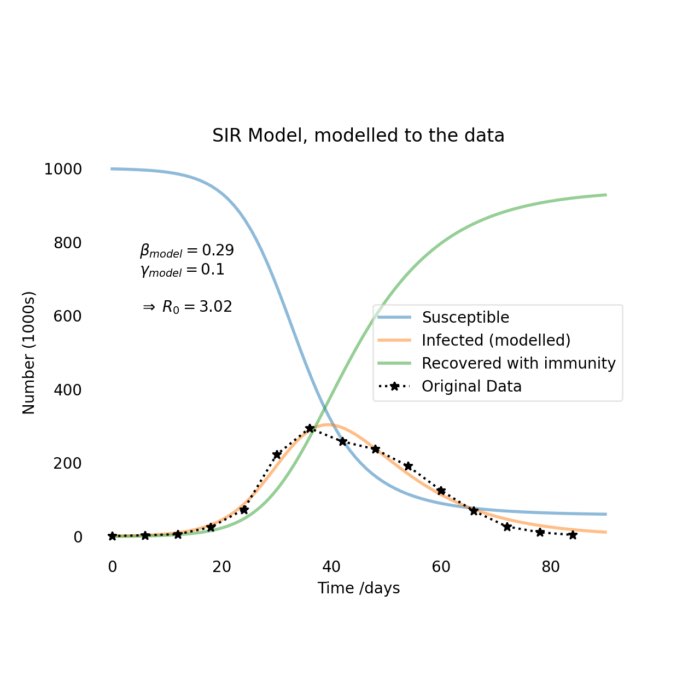
The SIR model: A mathematical approach to epidemic dynamics
In the wake of the COVID-19 pandemic, epidemiological models have garnered significant attention for their ability to provide insights into the spread and control of infectious diseases. One such model is the SIR model, forming the foundation for studying the dynamics of epidemics. In this blog post, we delve into the details of the SIR model, providing a mathematical description, and showcasing its application through a Python simulation.
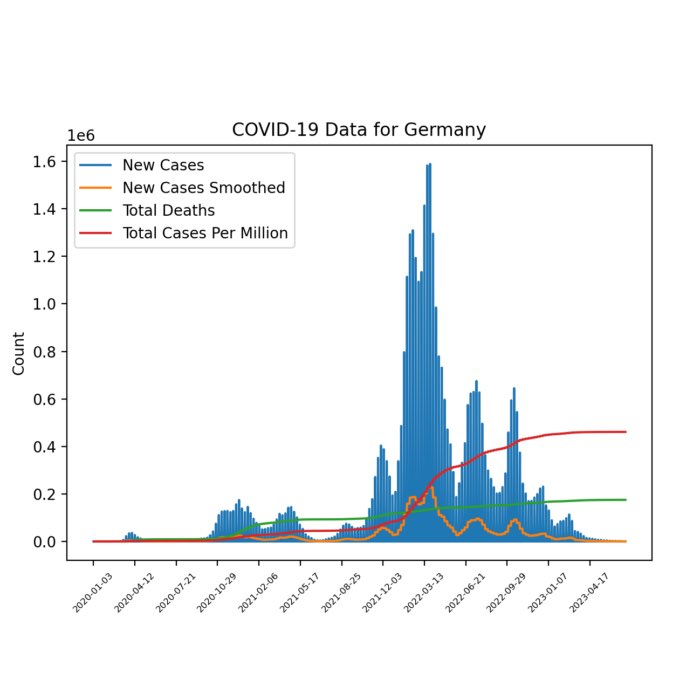
Interactive COVID-19 data exploration with Jupyter notebooks
Amidst the ongoing challenges of the COVID-19 pandemic, I have written a Jupyter notebook that facilitates interactive exploration of COVID-19 data. You can select specific countries and visualize key aspects such as confirmed cases, deaths, and vaccinations. The notebook is openly available on GitHub. Feel free to use and share it.
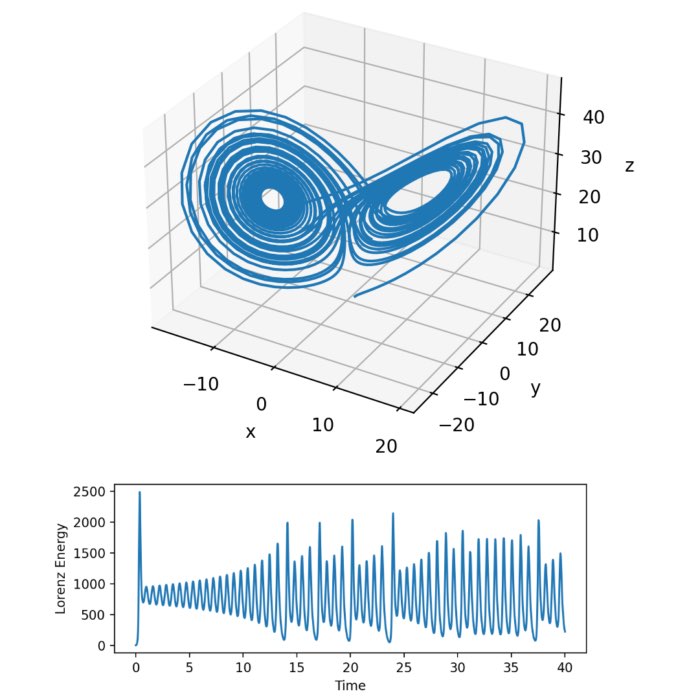
Solving the Lorenz system using Runge-Kutta methods
In my previous post, I introduced the Runge-Kutta methods for numerically solving ordinary differential equations (ODEs), that are challenging to solve analytically. In this post, we apply the Runge-Kutta methods to solve the Lorenz system. The Lorenz system is a set of differential equations known for its chaotic behavior and non-linear dynamics. By utilizing the Runge-Kutta methods, we can effectively simulate and analyze the intricate dynamics of this system.
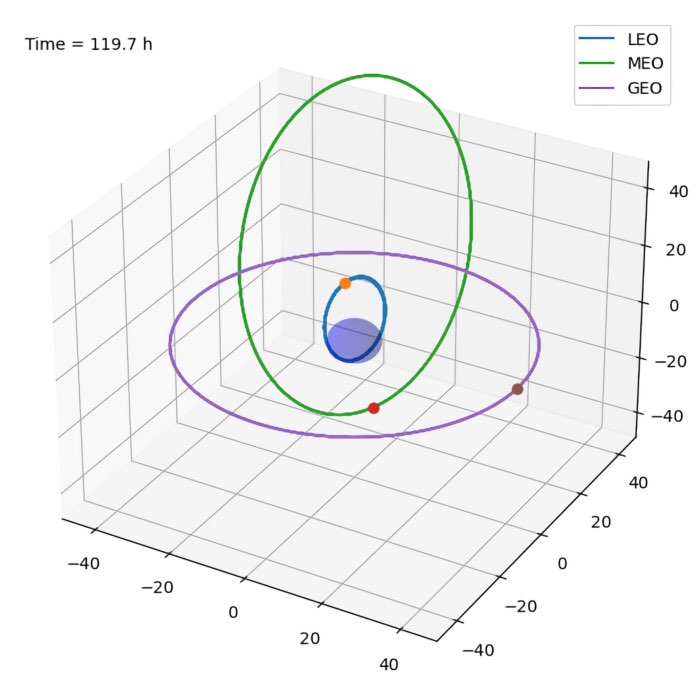
The two-body problem
The two-body system is a classical problem in physics. It describes the motion of two massive objects that are influenced by their mutual gravitational attraction. The two-body problem is a special case of the n-body problem, which describes the motion of two objects that are influenced by their mutual gravitational attraction. In this post, we make use of Runge-Kutta methods to solve the according equations of motion and simulate the trajectories of artificial satellites around the Earth.
Runge-Kutta methods for solving ODEs
In physics and computational mathematics, numerical methods for solving ordinary differential equations (ODEs) are of central importance. Among these, the family of Runge-Kutta methods stands out due to its versatility and robustness. In this post we compare the first four orders of the Runge-Kutta methods, namely RK1 (Euler’s method), RK2, RK3, and RK4.