Blog
Articles about computational science and data science, neuroscience, and open source solutions. Personal stories are filed under Weekend Stories. Browse all topics here. All posts are CC BY-NC-SA licensed unless otherwise stated. Feel free to share, remix, and adapt the content as long as you give appropriate credit and distribute your contributions under the same license.
tags · RSS · Mastodon · simple view · page 1/15
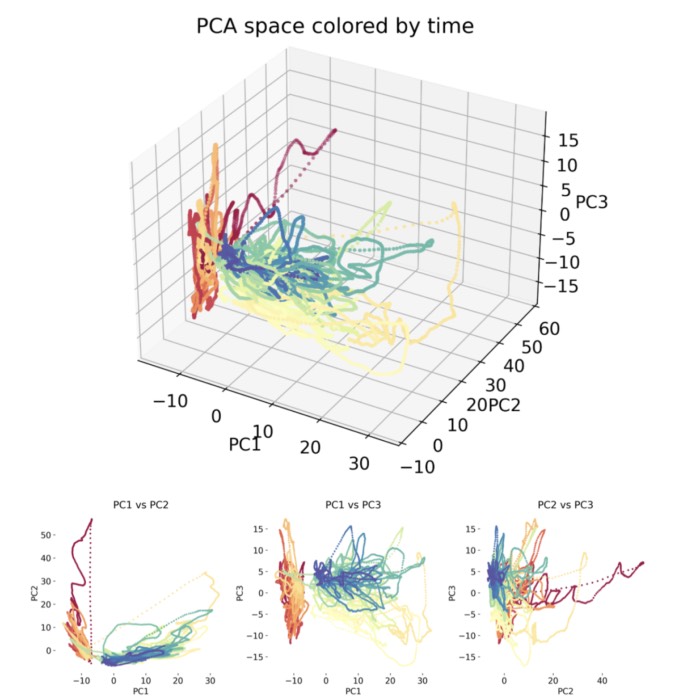
New teaching material: Dimensionality reduction in neuroscience
We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and I am pleased to announce that the full teaching material is now freely available under a Creative Commons (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.
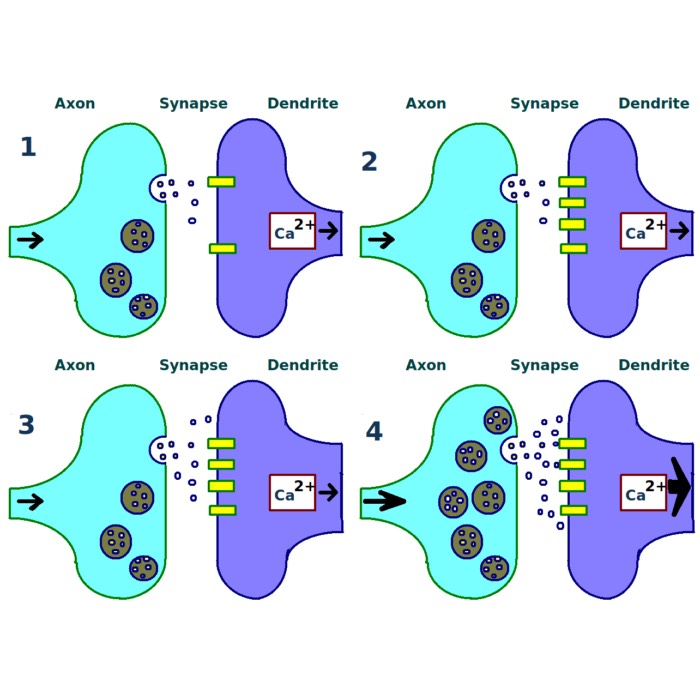
Long-term potentiation (LTP) and long-term depression (LTD)
Both long-term potentiation (LTP) and long-term depression (LTD) are forms of synaptic plasticity, which refers to the ability of synapses to change their strength over time. These processes are crucial for learning and memory, as they allow the brain to adapt to new information and experiences. Since we are often talking about both processes in the context of computational neuroscience, I thought it would be useful to provide a brief overview of biological mechanisms underlying these processes and their significance in the brain.
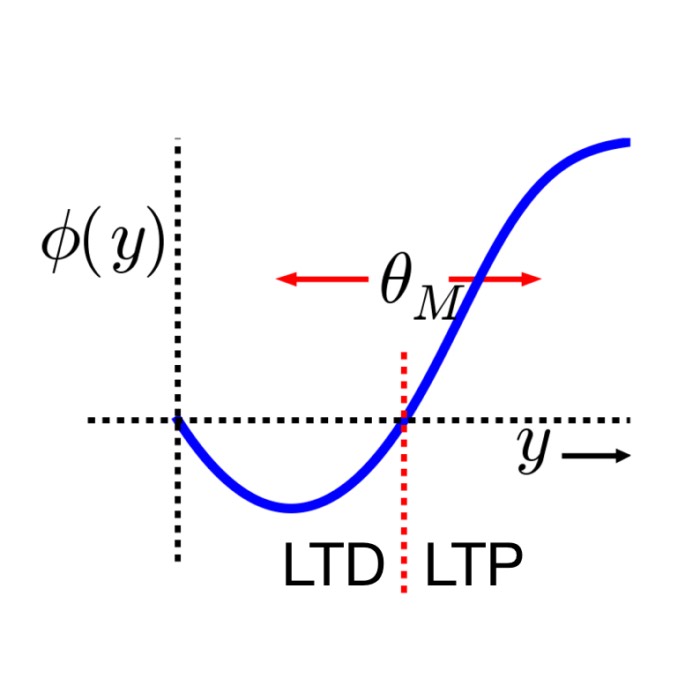
Bienenstock-Cooper-Munro (BCM) rule
The Bienenstock-Cooper-Munro (BCM) rule is a cornerstone in theoretical neuroscience, offering a comprehensive framework for understanding synaptic plasticity – the process by which connections between neurons are strengthened or weakened over time. Since its introduction in 1982, the BCM rule has provided critical insights into the mechanisms of learning and memory formation in the brain. In this post, we briefly explore and discuss the BCM rule, its theoretical foundations, mathematical formulations, and implications for neural plasticity.
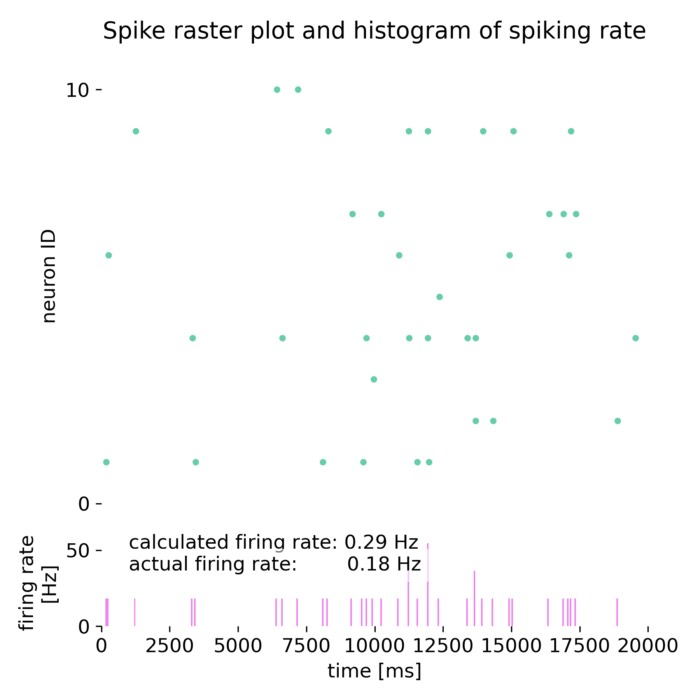
Campbell and Siegert approximation for estimating the firing rate of a neuron
The Campbell and Siegert approximation is a method used in computational neuroscience to estimate the firing rate of a neuron given a certain input. This approximation is particularly useful for analyzing the firing behavior of neurons that follow a leaky integrate-and-fire (LIF) model or similar models under the influence of stochastic input currents.
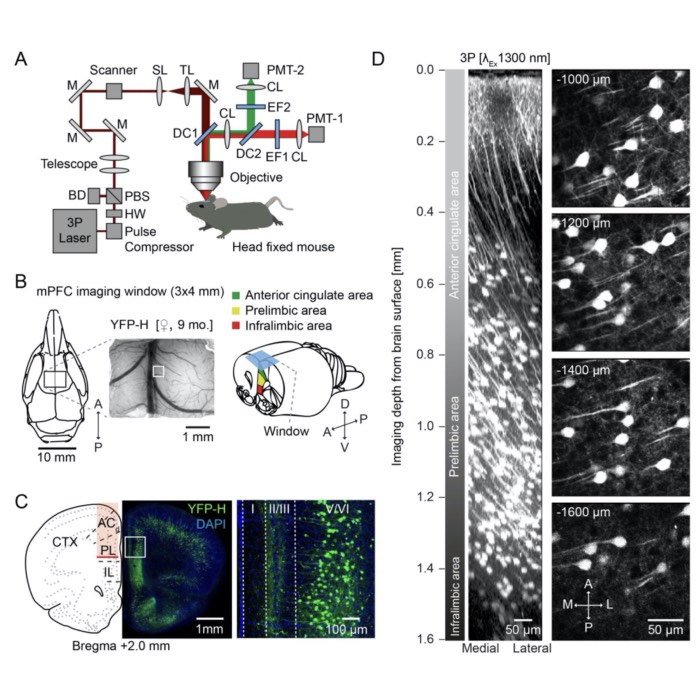
New preprint: Breaking new ground in brain imaging with three-photon microscopy
Our new preprint on Three-photon in vivo imaging of neurons and glia in the medial prefrontal cortex with sub-cellular resolution is out! In our study, we showcase the power of three-photon microscopy to probe deeper into the brain than ever before, achieving remarkable imaging depth and resolution in live, behaving animals.
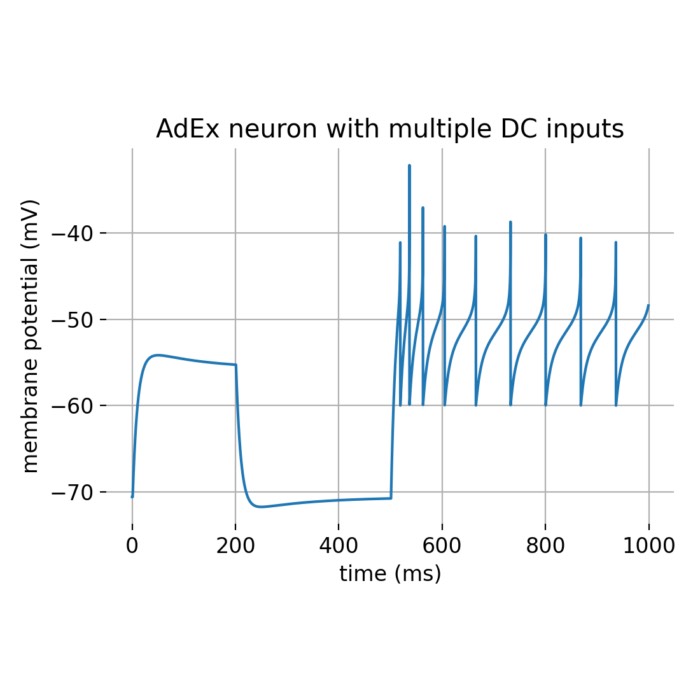
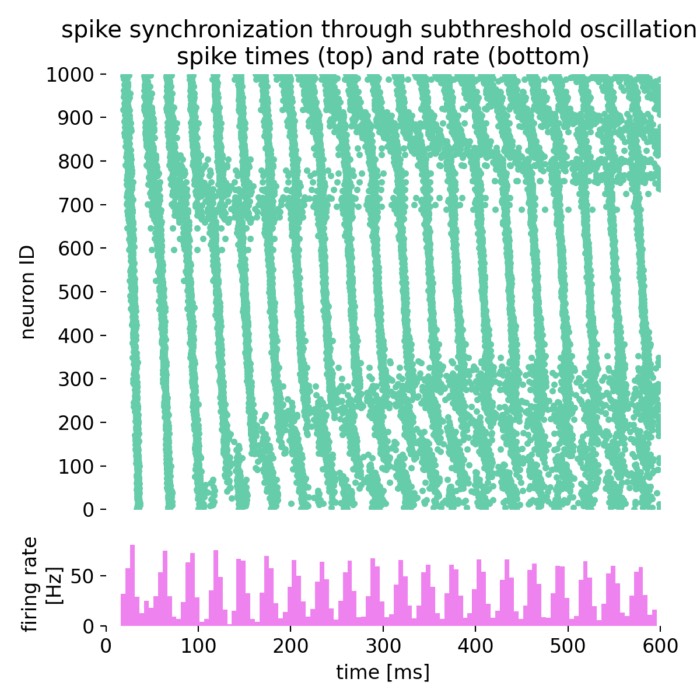
Exponential (EIF) and adaptive exponential Integrate-and-Fire (AdEx) model
The exponential Integrate-and-Fire (EIF) model is a simplified neuronal model that captures the essential dynamics of action potential generation. It extends the classical Integrate-and-Fire (IF) model by incorporating an exponential term to model the rapid rise of the membrane potential during spike initiation more accurately. The adaptive exponential Integrate-and-Fire (AdEx) model is a variant of the EIF model that includes an adaptation current to account for spike-frequency adaptation observed in real neurons. In this tutorial, we will explore the key features of the EIF and AdEx models and their applications in simulating neuronal dynamics.
Olfactory processing via spike-time based computation
In their work ‘Simple Networks for Spike-Timing-Based Computation, with Application to Olfactory Processing’ from 2003, Brody and Hopfield proposed a simple network model for olfactory processing. Brody and Hopfield showed how networks of spiking neurons (SNN) can be used to process temporal information based on computations on the timing of spikes rather than the rate of spikes. This is particularly relevant in the context of olfactory processing, where the timing of spikes in the olfactory bulb is crucial for encoding odor information. In this tutorial, we recapitulate the main concepts of Brody and Hopfield’s network using the NEST simulator.
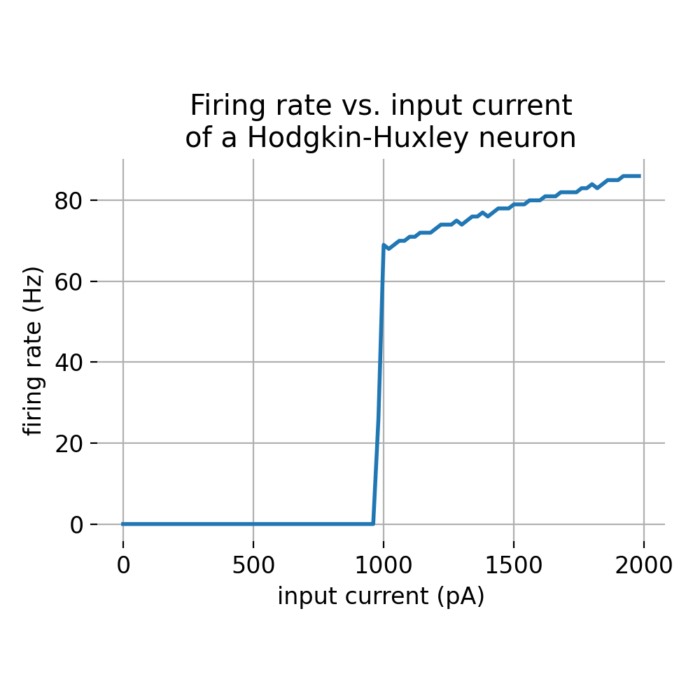
Frequency-current (f-I) curves
In this short tutorial, we will explore the concept of frequency-current (f-I) curves exemplified by the Hodgkin-Huxley neuron model. The f-I curve describes the relationship between the input current to a neuron and its firing rate. We will use the NEST simulator to simulate the behavior of a single Hodgkin-Huxley neuron and plot its f-I curve.
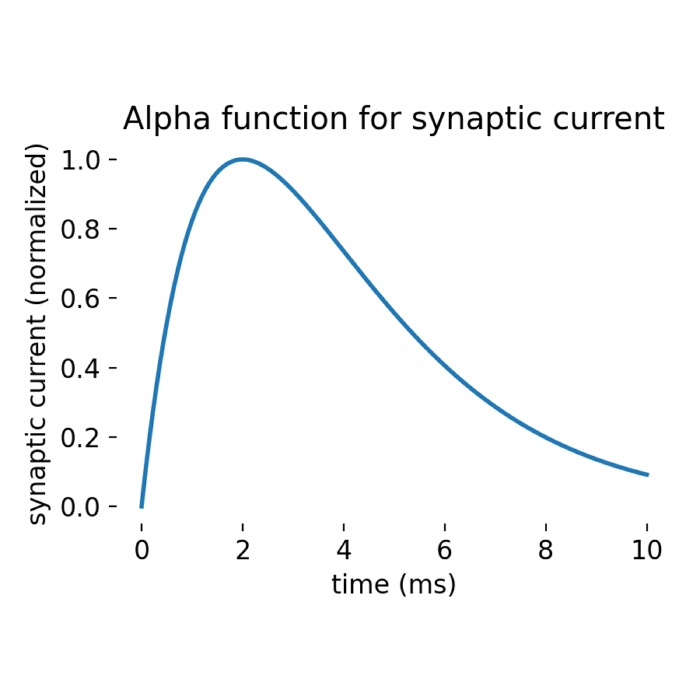
What are alpha-shaped post-synaptic currents?
In some recent posts, we have applied a specific type of integrate-and-fire neuron model, the
iaf_psc_alpha model implemented in the NEST simulator, to simulate the behavior of a single neuron or a population of neurons connected in a network. iaf_psc_alpha stands for ‘integrate-and-fire neuron with post-synaptic current shaped as an alpha function’. But what does ‘alpha-shaped current’ actually mean? In this short tutorial, we will explore the concept behind it.
Example of a neuron driven by an inhibitory and excitatory neuron population
In this tutorial, we recap the NEST tutorial ‘Balanced neuron example’. We will simulate a neuron driven by an inhibitory and excitatory population of neurons firing Poisson spike trains. The goal is to find the optimal rate for the inhibitory population that will drive the neuron to fire at the same rate as the excitatory population. This short tutorial is quite interesting as it is a practical demonstration of using the NEST simulator to model complex neuronal dynamics.