Blog
Articles about computational science and data science, neuroscience, and open source solutions. Personal stories are filed under Weekend Stories. Browse all topics here. All posts are CC BY-NC-SA licensed unless otherwise stated. Feel free to share, remix, and adapt the content as long as you give appropriate credit and distribute your contributions under the same license.
tags · RSS · Mastodon · simple view · page 3/16
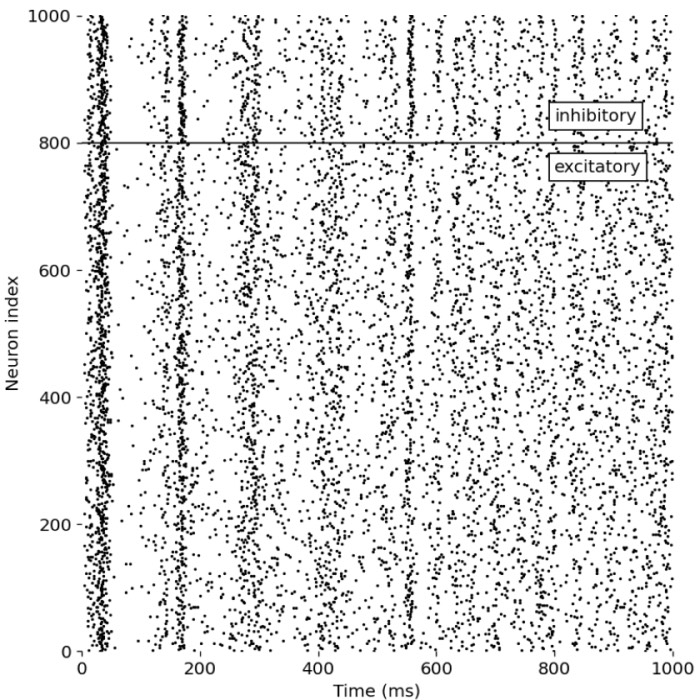
Brunel network: A comprehensive framework for studying neural network dynamics
In his work from 2000, Nicolas Brunel introduced a comprehensive framework for studying the dynamics of sparsely connected networks. The network is based on spiking neurons with random connectivity and differently balanced excitation and inhibition. It is characterized by a high level of sparseness and a low level of firing rates. The model is able to reproduce a wide range of neural dynamics, including both synchronized regular and asynchronous irregular activity as well as global oscillations. In this post, we summarize the essential concepts of that network and replicate the main results using the NEST simulator.
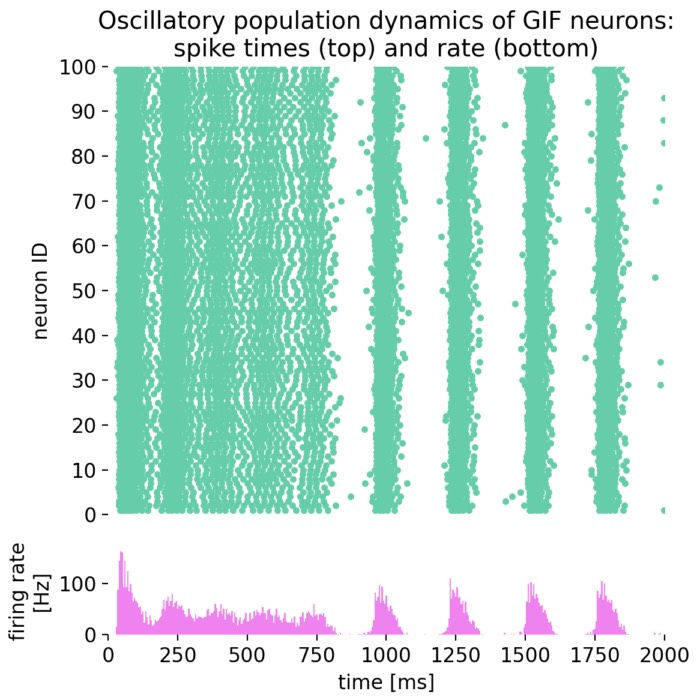
Oscillatory population dynamics of GIF neurons simulated with NEST
In this tutorial, we will explore the oscillatory population dynamics of generalized integrate-and-fire (GIF) neurons simulated with NEST. The GIF neuron model is a biophysically detailed model that captures the essential features of spiking neurons, including spike-frequency adaptation and dynamic threshold behavior. By simulating such a population of neurons, we can observe how these neurons interact and generate oscillatory firing patterns.
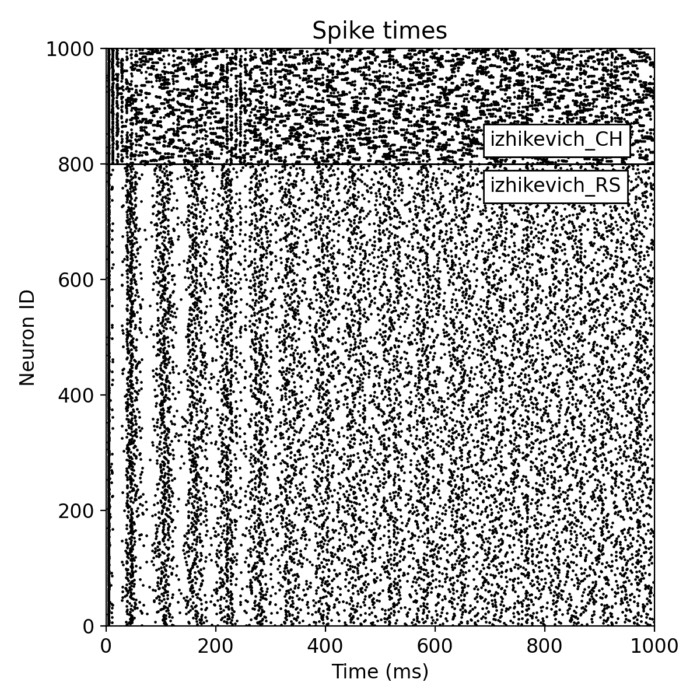
Izhikevich SNN simulated with NEST
In this post, we explore how easy it is to set up a large-scale, multi-population spiking neural network (SNN) with the NEST simulator. We simulate a simple SNN comprising two distinct populations of Izhikevich neurons, demonstrating the efficiency and flexibility of NEST and its capability to handle complex neural network simulations with ease.
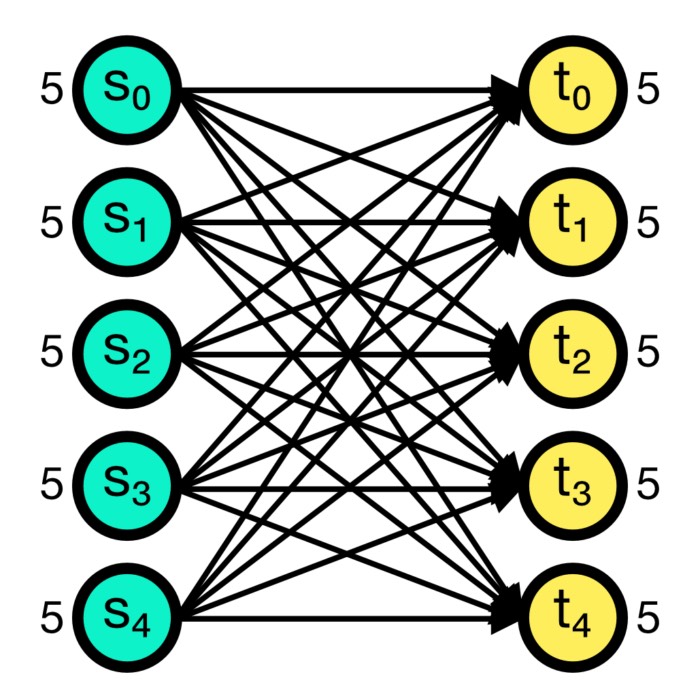
Connection concepts in NEST
In the previous post, we learned about the basic concepts of the NEST simulator and how to create a simple single neuron model. This time, we will take a closer look at the connection concepts in NEST, which are crucial for building more complex neural networks.
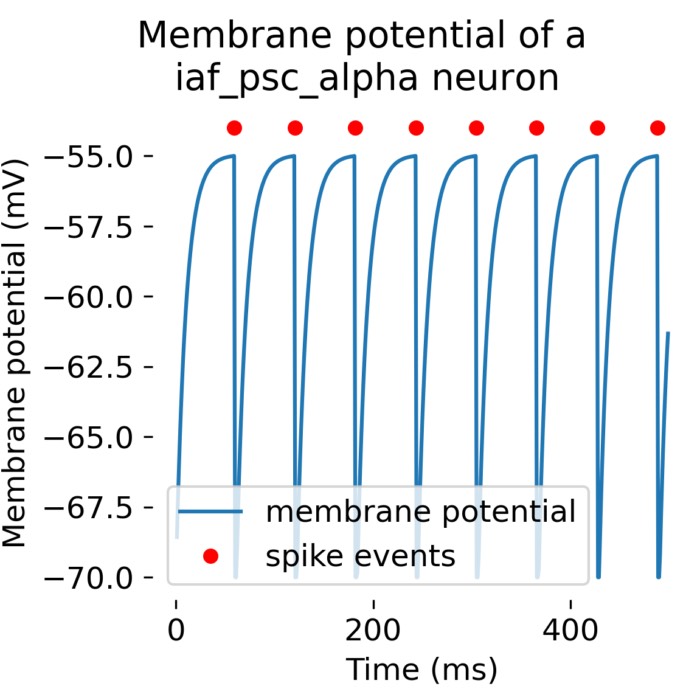
Step-by-step NEST single neuron simulation
While NEST is designed for large-scale simulations of neural spike networks, the underlying models are based on approximating the behavior of single neurons and synapses. Before using NEST for network simulations, it is probably helpful to first understand the basic functions of the software tool by modelling and studying the behavior of individual neurons. In this tutorial, you will learn about NEST’s concept of nodes and connections, how to set up a neuron model of your choice, how to change model parameters, which different stimulation paradigms are included in NEST and how to record and analyze the simulation results.
NEST simulator – A powerful tool for simulating large-scale spiking neural networks
The NEST simulator is a powerful software tool designed for simulating large-scale networks of spiking neurons (SNN). It has become an essential instrument in the field of computational neuroscience, providing the capability to model, simulate, and analyze the complex dynamics of neuronal systems. And it comes with a user-friendly Python interface, facilitating the construction of neuronal networks with minimal effort.
Simulating spiking neural networks with Izhikevich neurons
The Izhikevich neuron model that we have discussed earlier is known for its simplicity and computational efficiency as well as for its biological plausibility. The model is based on two coupled differential equations that describe the membrane potential and the recovery variable of a neuron. The model can reproduce a wide range of spiking behaviors observed in real neurons, such as regular spiking, fast spiking, chattering, and more. In this post, we explore how we can quickly set up a spiking neural network (SNN) simulation using the Izhikevich neuron model in Python.
Izhikevich model
Computational neuroscience utilizes mathematical models to understand the complex dynamics of neuronal activity. Among various neuron models, the Izhikevich model stands out for its ability to combine biological fidelity with computational efficiency. Developed by Eugene Izhikevich in 2003, this model simulates the spiking and bursting behavior of neurons with a remarkable balance between simplicity and biological relevance. In this post, we explore the properties of the Izhikevich model, examining its application and adaptability in simulating single neuron behaviors.
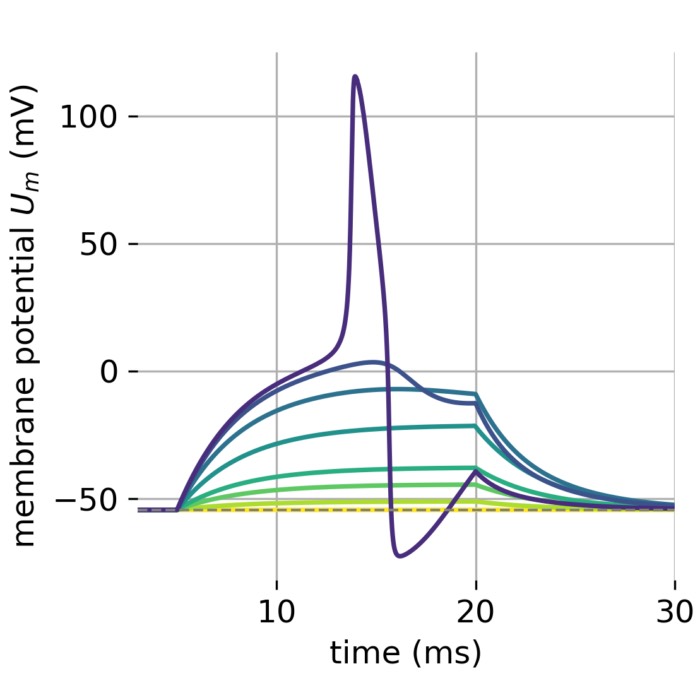
Hodgkin-Huxley model
An important step beyond simplified neuronal models is the Hodgkin-Huxley model. This model is based on the experimental data of Hodgkin and Huxley, who received the Nobel Prize in 1963 for their groundbreaking work. The model describes the dynamics of the membrane potential of a neuron by incorporating biophysiological properties instead of phenomenological descriptions. It is a cornerstone of computational neuroscience and has been used to study the dynamics of action potentials in neurons and the behavior of neural networks. In this post, we derive the Hodgkin-Huxley model step by step and provide a simple Python implementation.
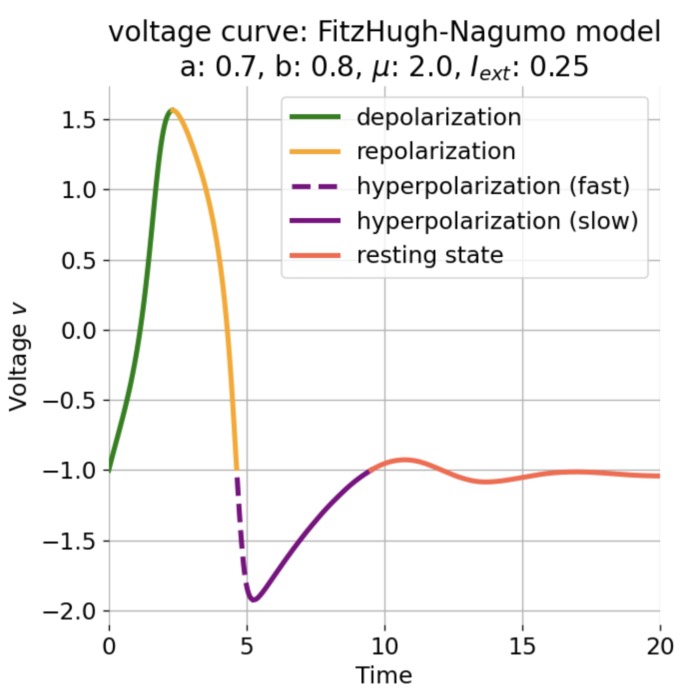
FitzHugh-Nagumo model
In the previous post, we analyzed the dynamics of Van der Pol oscillator by using phase plane analysis. In this post, we will see, that this oscillator can be considered as a special case of another dynamical system, the FitzHugh-Nagumo model. The FitzHugh-Nagumo model is a simplified model used to describe the dynamics of the action potential in neurons. With a few modifications of the Van der Pol equations we can obtain the model’s ODE system. By again using phase plane analysis, we can then investigate how the dynamics of the system changes under these modifications.