Integrate and Fire Model: A simple neuronal model

Studying the brain involves understanding the intricate activity of billions of interconnected neuronsꜛ, the fundamental units of the brain. One useful tool in this endeavor is the Integrate-and-Fire model, a simplified representation of neuronal behavior. This model approximates the changes in a neuron’s membrane potentialꜛ in response to an input current. If the membrane potential reaches a threshold, the neuron ‘fires’ a signal, also known as an action potentialꜛ, to other neurons and then resets. While a simplification, the model captures essential dynamics of neuronal firing and provides a computationally efficient approach to simulate and explore the behavior of large neuronal networks, aiding our understanding of brain function. In this blog post, we explore the model and run some simulations in Python to see how it works.

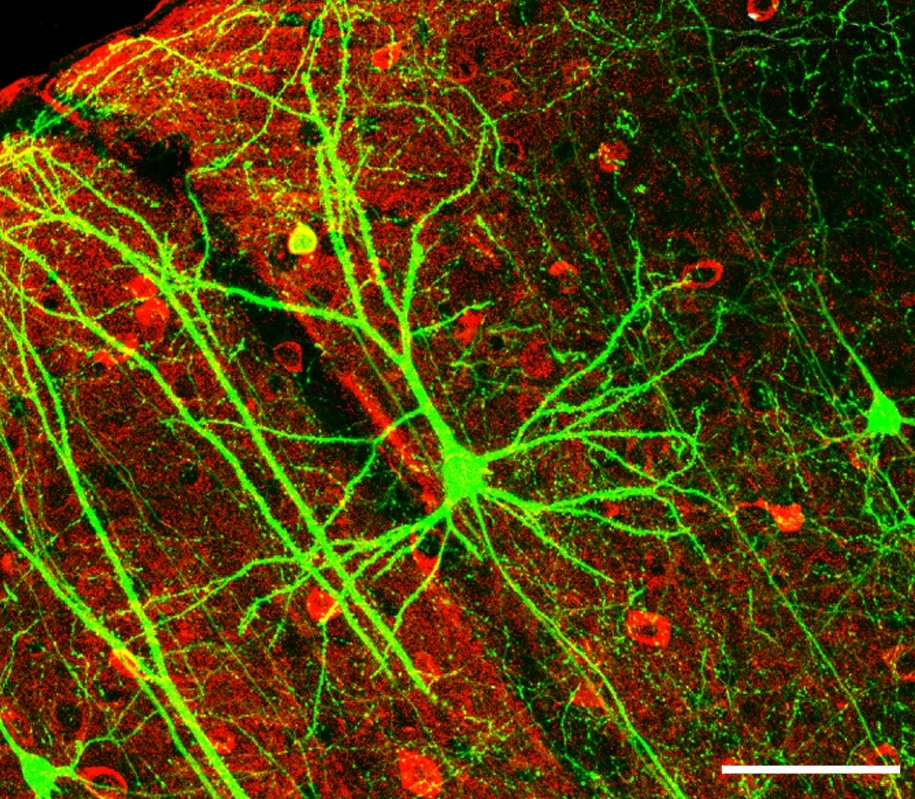Pyramidal cell with a large dendrite tree in the cerebral cortex of a mouse expresses green fluorescent protein. GABA-producing interneurons are shown in red. (Length of the scale at the bottom right: 100 µm). Source: Wikimediaꜛ (CC BY 2.5 license), originally from Wei-Chung et al. (2005)ꜛ

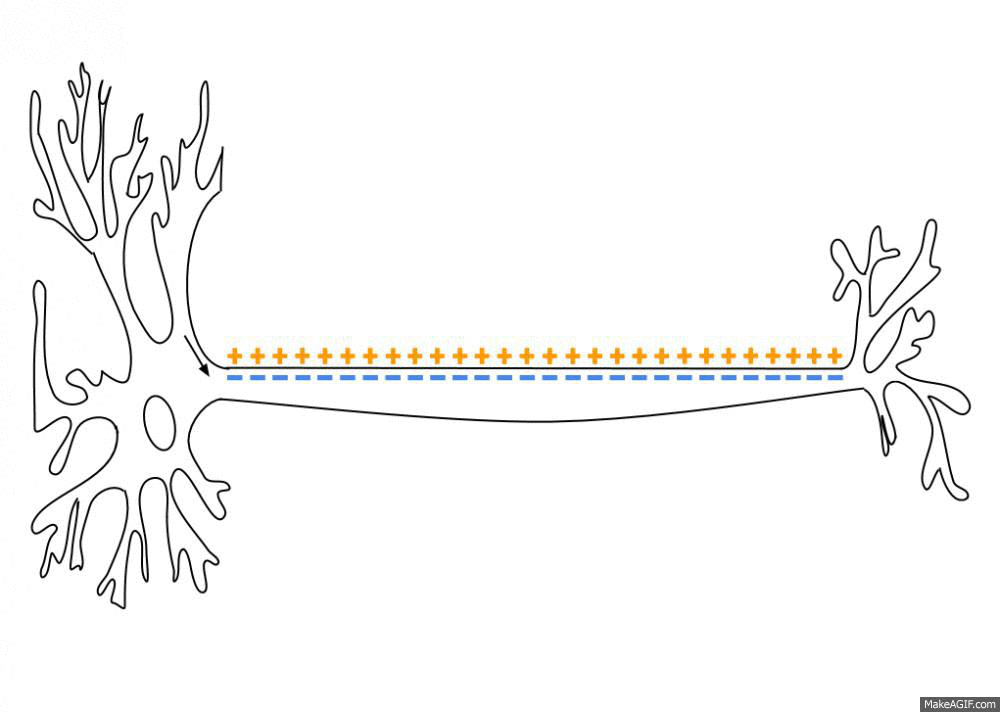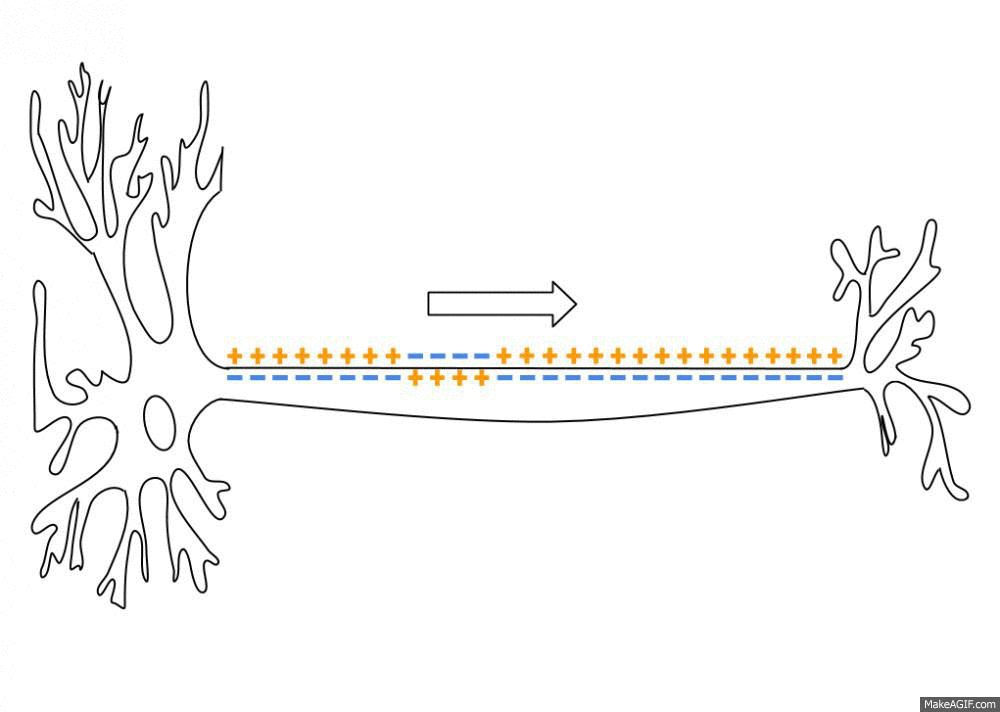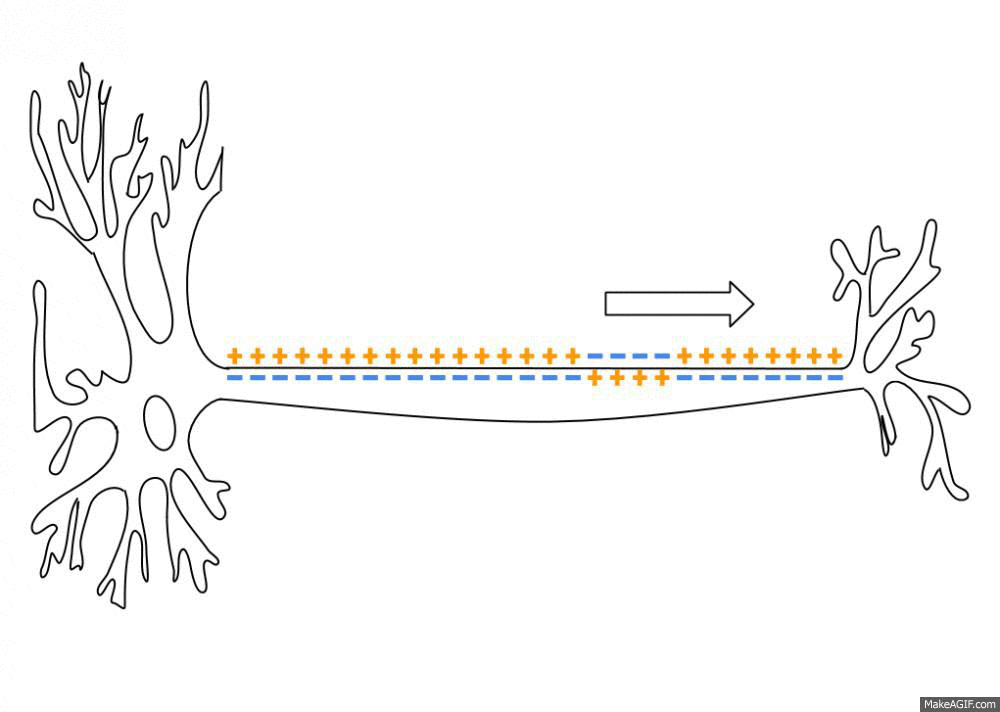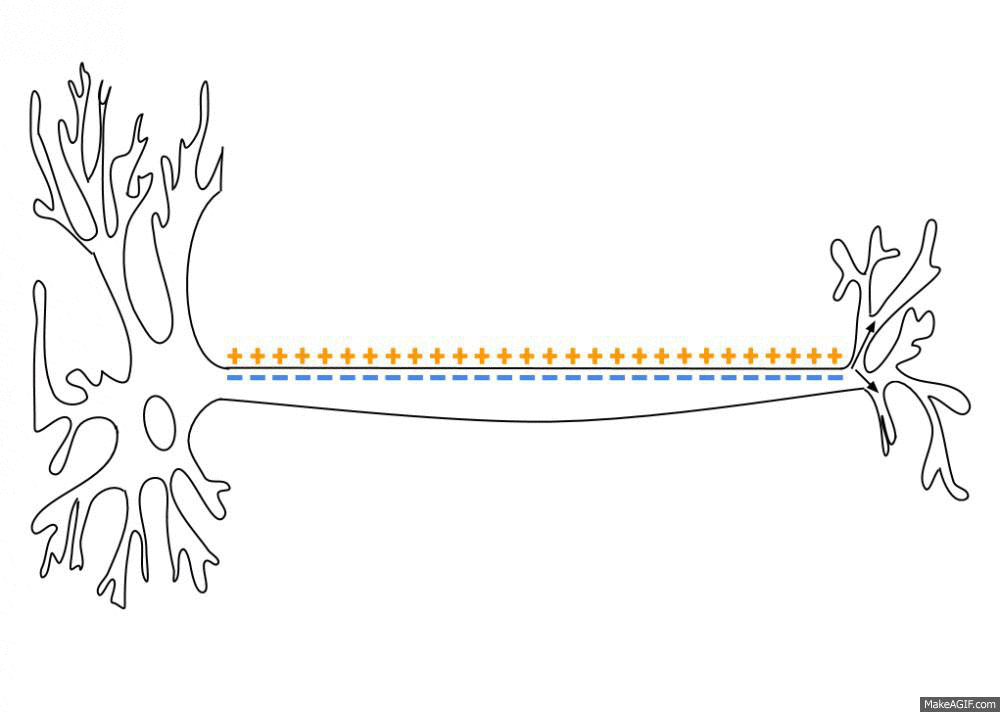Animation of an action potential (AP). While the AP travels down an axonꜛ there is a change in electric polarity across the membrane of the axon. In response to a signal from another neuron, sodium- (Na⁺) and potassium- (K⁺)–gated ion channelsꜛ open and close as the membrane reaches its threshold potential. Na⁺ channels open at the beginning of the AP, and Na⁺ moves into the axon, causing depolarization. Repolarization occurs when K⁺ channels open and K⁺ moves out of the axon, creating a change in electric polarity between the outside of the cell and the inside. The impulse travels down the axon in one direction only, to the axon terminal where it signals other neurons. Source: Wikimediaꜛ (CC BY-SA 3.0 license)

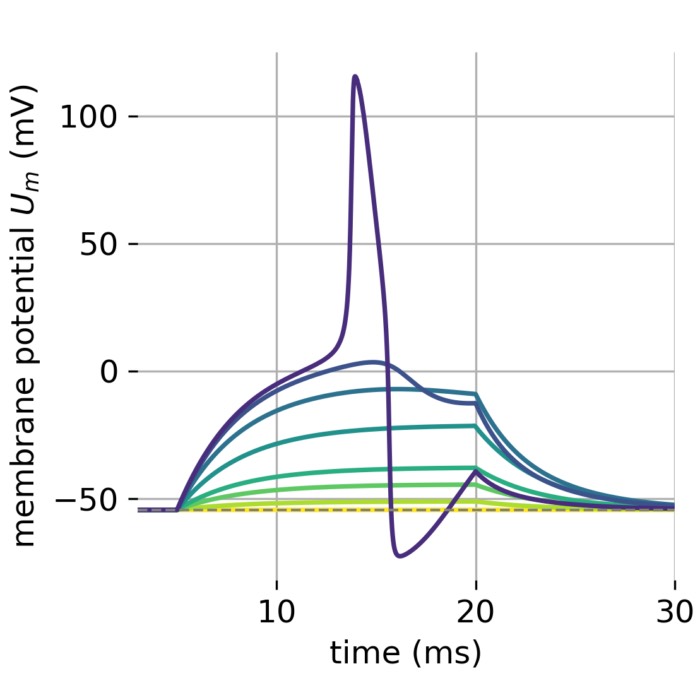
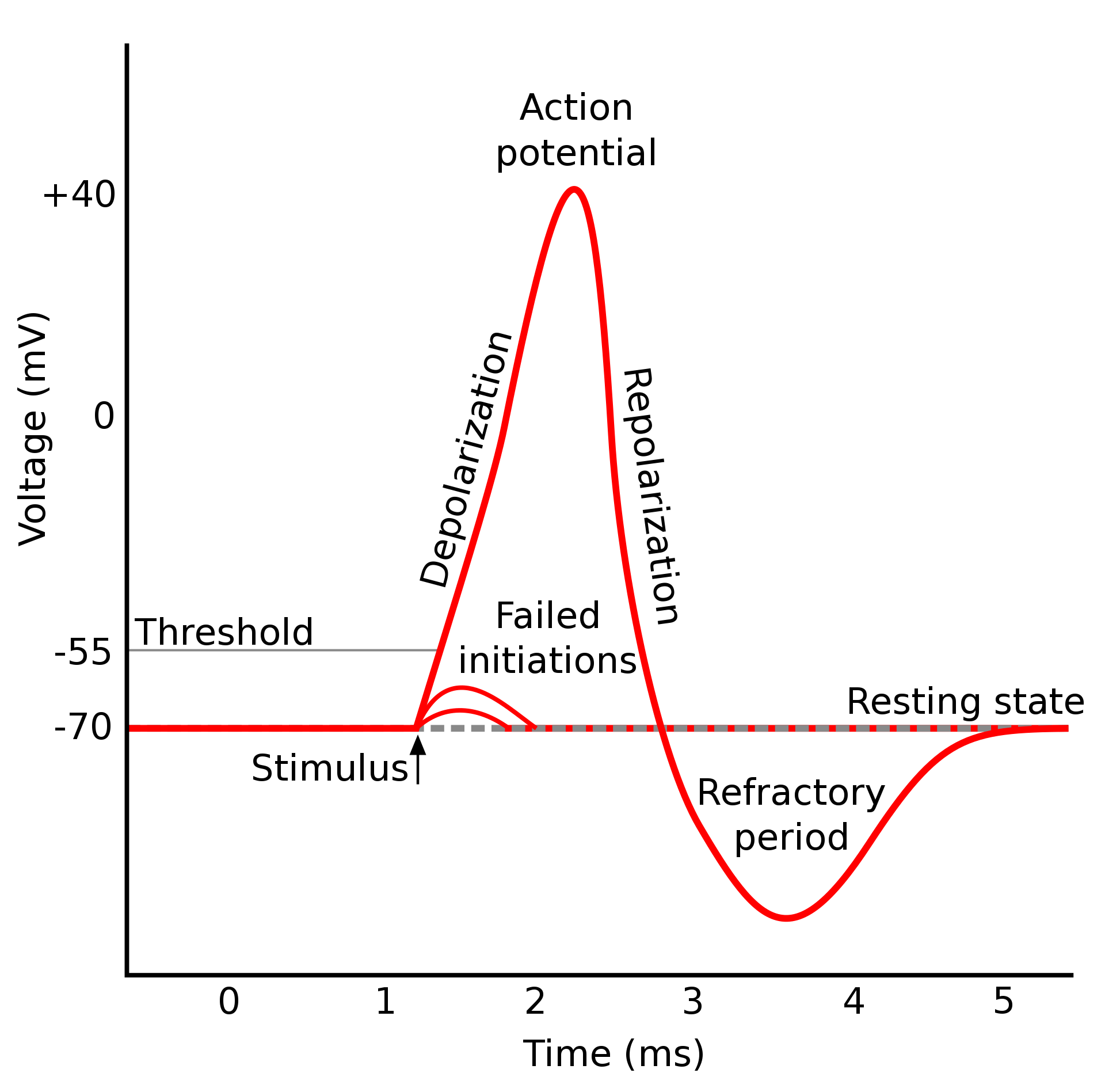Shape of a typical action potential. The membrane potential starts at −70 mV. A stimulus is applied at time = 1 ms, which raises the membrane potential above −55 mV (the threshold potential), which rapidly rises to a peak potential of +40 mV at time = 2 ms. Just as quickly, the potential then drops and overshoots to −90 mV at time = 3 ms, and finally the resting potential of −70 mV is reestablished at time = 5 ms. Wikimediaꜛ (CC BY-SA 3.0 license)

The model

The Integrate-and-Fire model is primarily based on the properties of an electrical circuit that represents a neuron. The neuron is depicted as a capacitor, which can accumulate and store charge. The basic electrical circuit representing a leaky integrate-and-fire model consists of a capacitor, representing the membrane’s capacity to store charge, and a resistor, representing the membrane’s resistance to current flow. This model captures the essential features of a neuron’s response to incoming signals. When the neuron receives an input current, the membrane voltage changes. The Integrate-and-Fire model describes how the neuron integrates these incoming signals over time and fires an action potential once the membrane voltage exceeds a certain threshold.

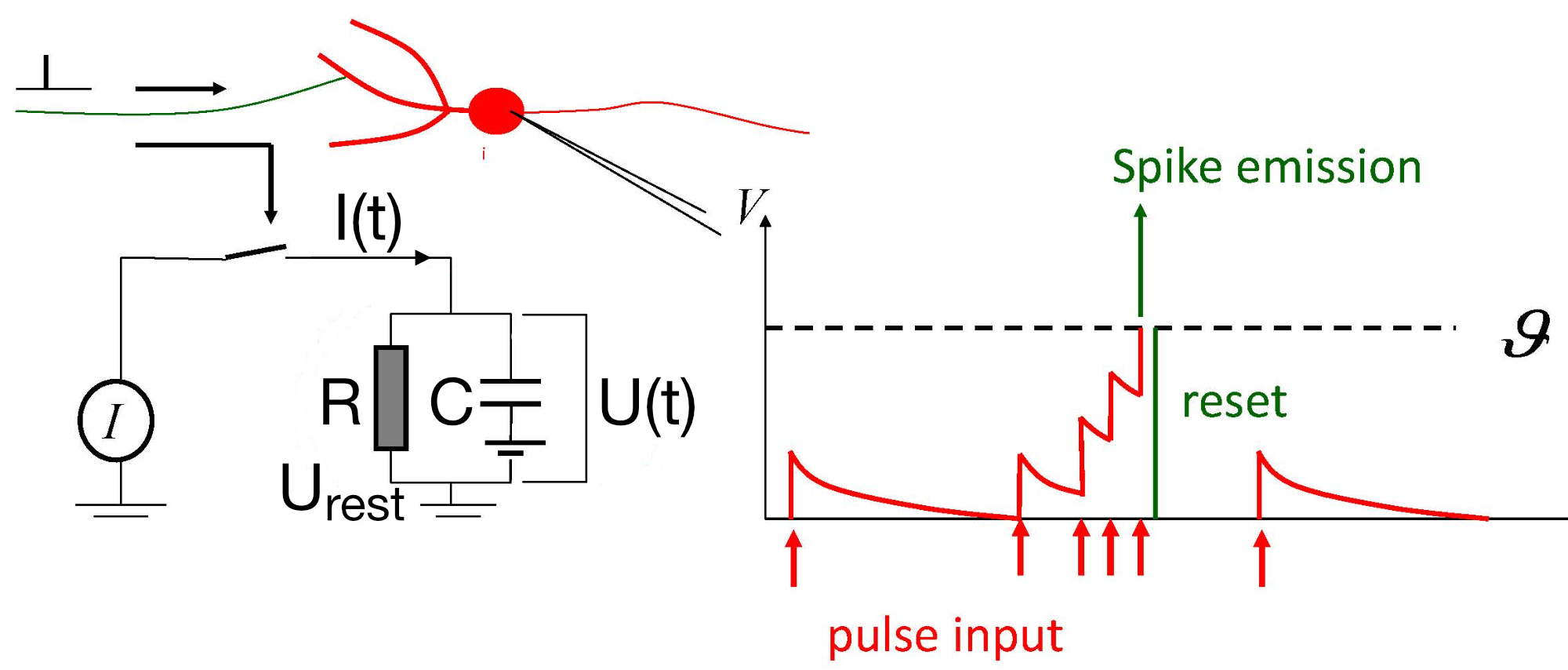Left: RC equivalent circuit of an Integrate-and-Fire model neuron. The “neuron” in this model is represented by the capacitor $C$ and the resistor $R$. The membrane potential $U(t)$ is the voltage across the capacitor $C$. The input current $I(t)$ is split into a resistive current $I_R$ and a capacitive current $I_C$ (not shown here). The resistive current is proportional to the voltage difference across the resistor $R$. The capacitive current is proportional to the rate of change of voltage across the capacitor. $U_\text{rest}$ is the resting potential of the neuron, which is the membrane potential when the neuron is not receiving any input. Right: The response $U(t)$ on current pulse inputs. When the neuron receives an input current, the membrane voltage changes. The Integrate-and-Fire model describes how the neuron integrates these incoming signals over time and fires an action potential once the membrane voltage exceeds a certain threshold (here depicted as $\vartheta$). Modified from this source: Wikimediaꜛ (CC BY-SA 4.0 license)

In order to derive an equation that links the momentary voltage to the input current, we consider the described electrical circuit, use the law of current conservation and split the driving current into two components. The first component is the resistive current, which is proportional to the voltage difference across the resistor. We can denote this as:

\[I_R = {U_R \over R} = { {U(t) - U_\text{rest} } \over R}\]

where $I$ is the current, $U_R = U(t) - U_\text{rest}$ is the voltage along the resistance, and $R$ is the resistance. $U_\text{rest}$ is the resting potential of the neuron, which is the membrane potential when the neuron is not receiving any input.

The second component is the capacitive current, which is proportional to the rate of change of voltage across the capacitor:

\[I_C=C{dU(t) \over dt}\]

where $C$ is the capacitance and $dU/dt$ is the change of voltage with respect to time $t$.

The total current is the sum of the resistive and capacitive currents:

\[I(t) = I_C+I_R = { {U(t) - U_\text{rest} } \over R} + C{dU(t) \over dt}\] \[\Leftrightarrow \; C{dU(t) \over dt} = - { {U(t) - U_\text{rest} } \over R} + I(t)\]

Multiplying by $R$ and introducing the time constant $\tau := RC$, we get:

\[\Leftrightarrow \; RC{dU(t) \over dt} = - (U(t) - U_\text{rest}) + RI(t)\] \[\Leftrightarrow \; \tau {dU(t) \over dt} = - (U(t) - U_\text{rest}) + RI(t)\]

This is the standard equation of the leaky Integrate-and-Fire model, which describes the change of the membrane potential $U(t)$ over time. The term “leaky” refers to the fact that the model integrates its input currents over time, but the voltage tends to “leak” back towards zero, which reflects the loss of charge across the membrane due to resistive currents.

By resubstituting of $U_R(t) = U(t) - U_\text{rest}$ we get

\[\tau {dU_R(t) \over dt} = - U_R(t) + RI(t)\]

which is another form of the equation commonly used in the literature, where $U_R$ is sometimes also denoted as $V$.

The equation is a first-order linear differential equation, and we can derive an analytical solution using an exponential function. Assuming that at time $t=0$, the voltage across the membrane is $U_0$, and there’s no input current, i.e., $I(t) = 0$, the solution of the differential equation is given by:

\[U_R(t) = U(t) - U_\text{rest} = U_0 e^{-\frac{t-t_0}{\tau} }\]

for $t \geq t_0$. This equation shows that in the absence of an input, the membrane potential decays exponentially towards the resting potential $U_\text{rest}$ with a time constant $\tau$. The time constant $\tau$ is a measure of the membrane’s resistance to current flow. The larger the time constant, the slower the membrane potential decays towards the resting potential.

In the presence of a time-dependent input current $I(t)\neq 0$, the neuron’s voltage changes in response to this input. In this case, the solution of the Integrate-and-Fire model is given by:

\[U(t) = U_\text{rest} + \frac{R}{\tau} \int_0^\infty I(t') e^{-\frac{t-t'}{\tau}} dt'\]

The above equation describes the membrane potential $U(t)$ at time $t$ as a function of the time-dependent input current $I(t)$. $I(t)$ is often simulated as a step function, i.e., $I(t) = I_0$ for $t \geq t_0$ or a sinusoidal function, i.e., $I(t) = I_0 \sin(\omega t)$, where $I_0$ is the amplitude of the input current and $\omega$ is the frequency of the input current.

The term $e^{-(t-t’)/\tau_m}$ serves as a ‘memory kernel’, giving more weight to recent inputs (as time $t’$ approaches $t$) and less weight to older inputs (as $t’$ is far from $t$).

When a firing threshold $U_{th}$ is added to the model, the voltage resets after reaching this threshold, which is incorporated into the equation by introducing a new term:

\[U(t) = U_\text{rest} + \frac{R}{\tau} \int_0^\infty (I(t') - I_\text{reset}) e^{-\frac{t-t'}{\tau}} dt'\]

Here, $I_{reset}$ represents the resetting current that fires whenever the membrane potential reaches the threshold $U_{th}$. This equation is often expressed using a Dirac delta function:

\[U(t) = U_\text{rest} + \frac{R}{\tau} \int_0^\infty (I(t')\; -\] \[\; \sum_n \delta(t' - t^{(n)}) \; e^{-\frac{t-t'}{\tau}} dt'\]

The sum $\sum_n$ runs over all firing times $t^{(n)}$ before time $t$. The reset current $I_{reset}$ is defined as:

\[I_\text{reset} = \frac{1}{R} (U_{th} - U_\text{rest} - RI(t^{(n)}))\]

In simple terms, the reset current $I_\text{reset}$ is the amount of current needed to bring the neuron’s potential down from the threshold $U_{th}$ back to the resting potential $U_\text{rest}$ immediately after a firing event at time $t^{(n)}$

Simulating with Python

To better understand the dynamics of the Integrate-and-Fire model, I’ve written some simple Python code to simulate the Integrate-and-Fire model incorporating the equations above. I used a basic Euler method for numerical integration, which might not be accurate for large time steps or fast dynamics. For a more accurate simulation, you might want to use a more sophisticated method like Runge-Kutta or use a library like Brian2ꜛ that is specifically designed for simulating spiking neural networks.

The code is implemented in an interactive Jupyter notebook and you can change the parameters of the model using sliders. You can run the notebook in Google Colab or Binder by clicking on one of the buttons below:

Or download the notebook from this GitHub repositoryꜛ and run it locally.

The code models a single Integrate-and-Fire neuron for different input currents $I(t)$. First, the membrane potential $U(t)$ and corresponding spike times are calculated using the equation for a constant input current $I(t) = I_0$:

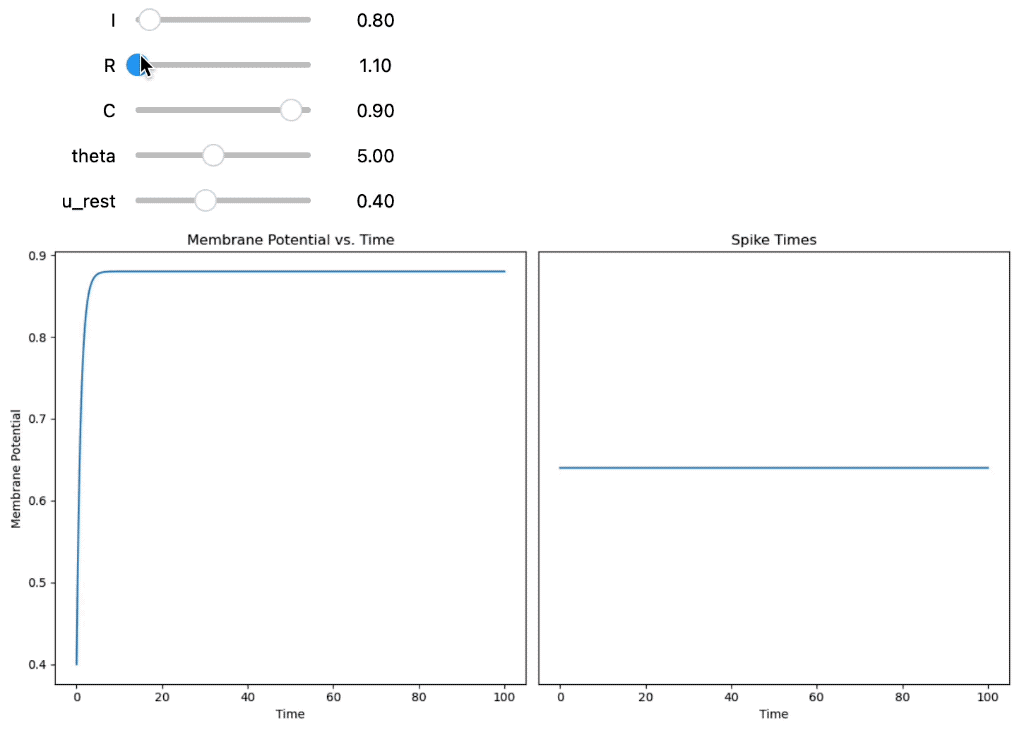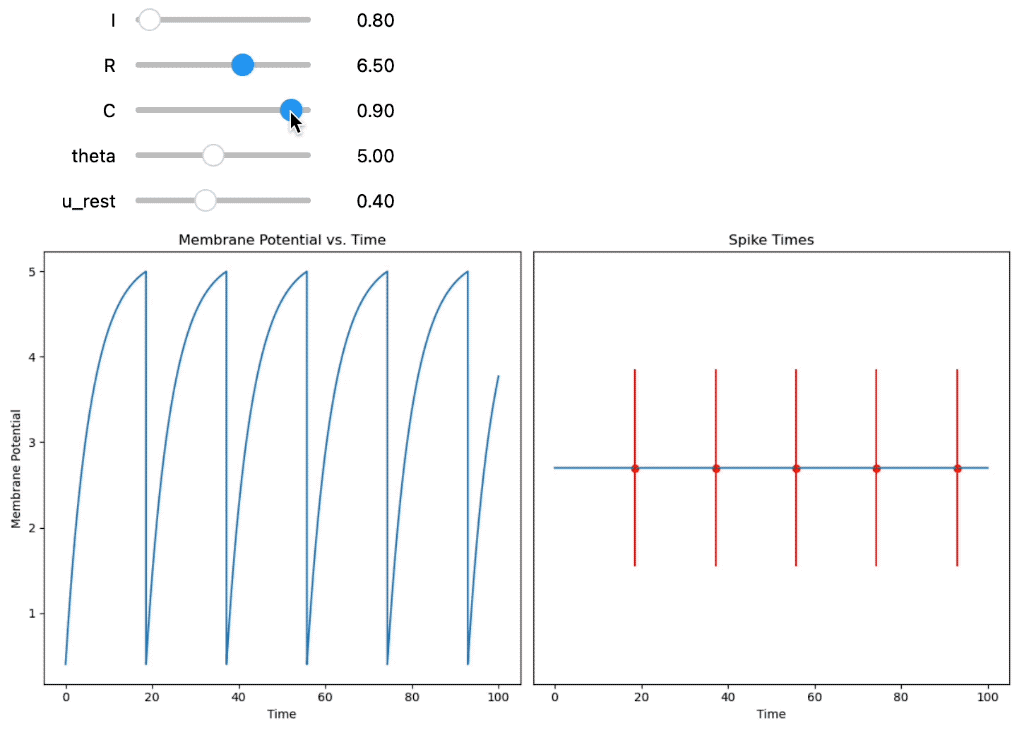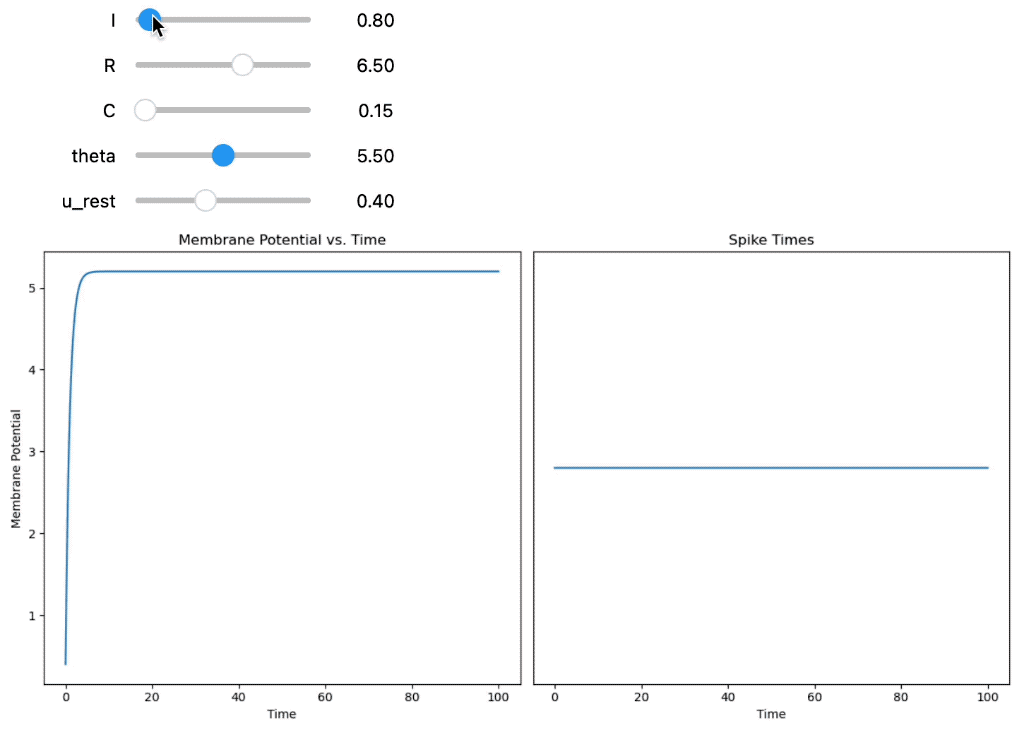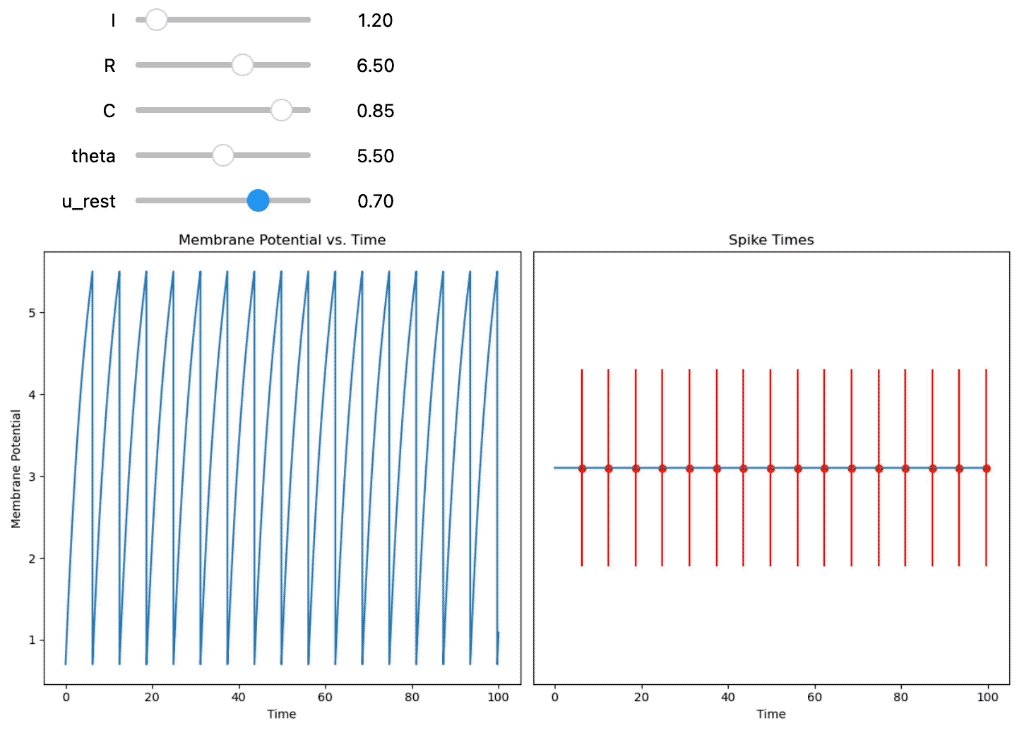Integrate-and-Fire neuron using a constant input current $I(t) = I_0$. You can interactively adjust the parameters of the model using the sliders, namely $I_0$, the resistance $R$, the capacity $C$, the firing threshold $theta§$ and the resting potential $U_\text{rest}$.

Second, the membrane potential $U(t)$ and corresponding spike times are calculated using the equation for a time-variable input current $I(t)$:

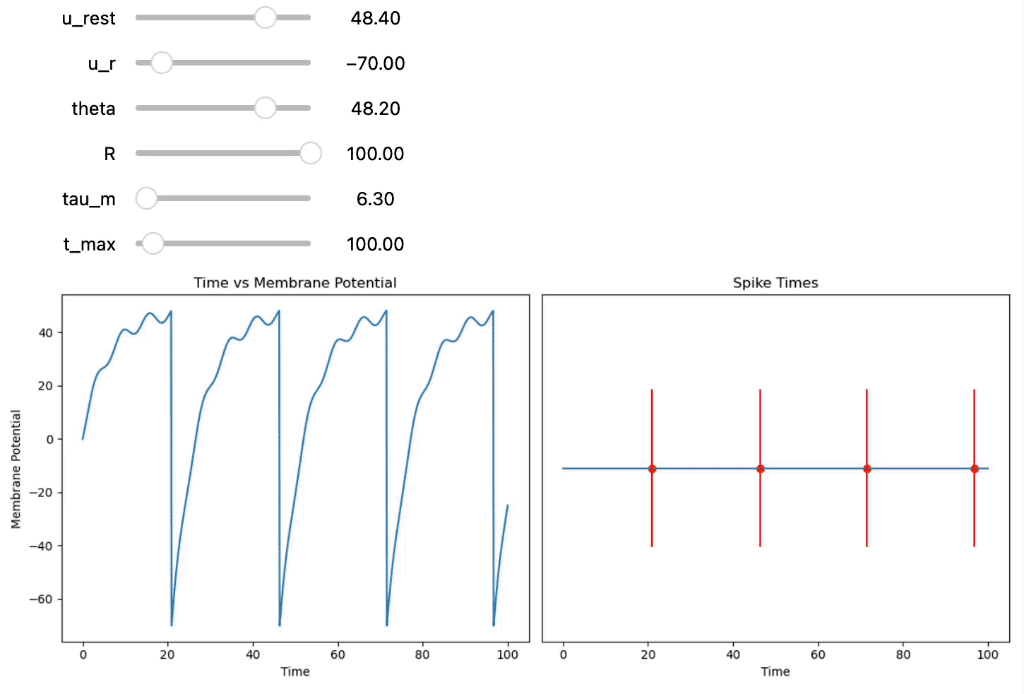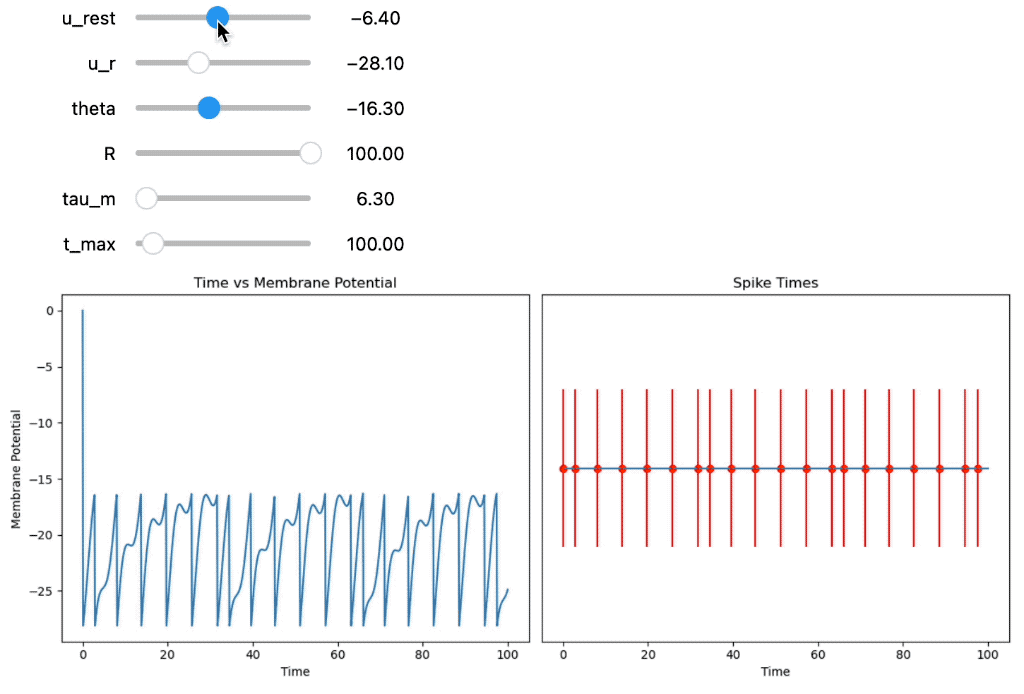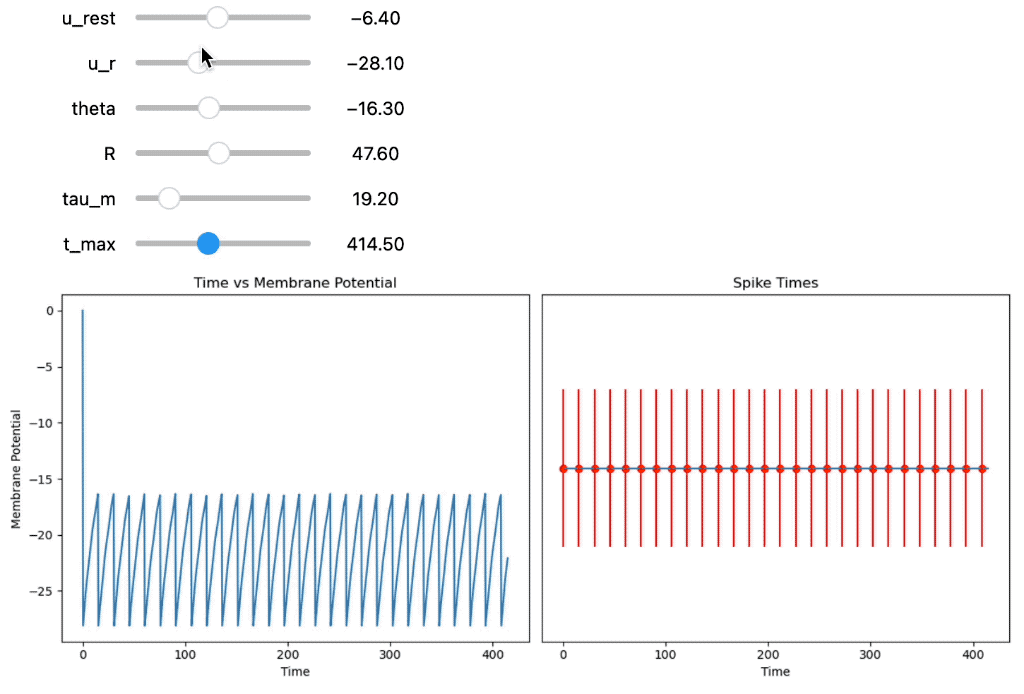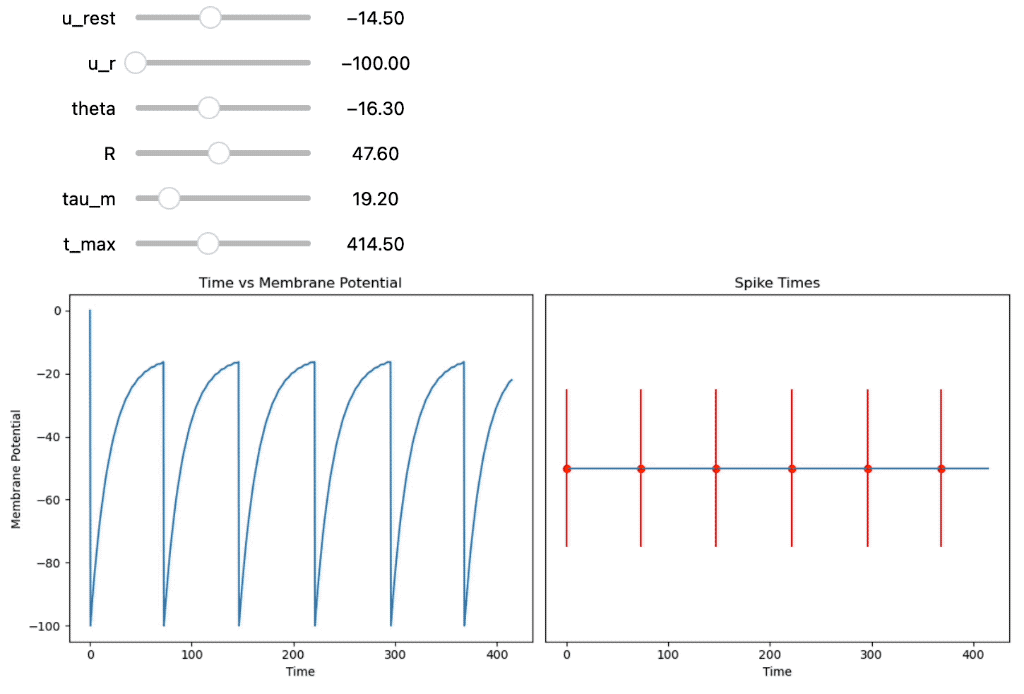Integrate-and-Fire neuron using a time-dependent input current $I(t)$. You can additionally adjust the membrane time constant $\tau$.

Third, the membrane potential $U(t)$ and corresponding spike times are calculated for two constant input currents $I_{0,1}$ and $I_{0,2}$:

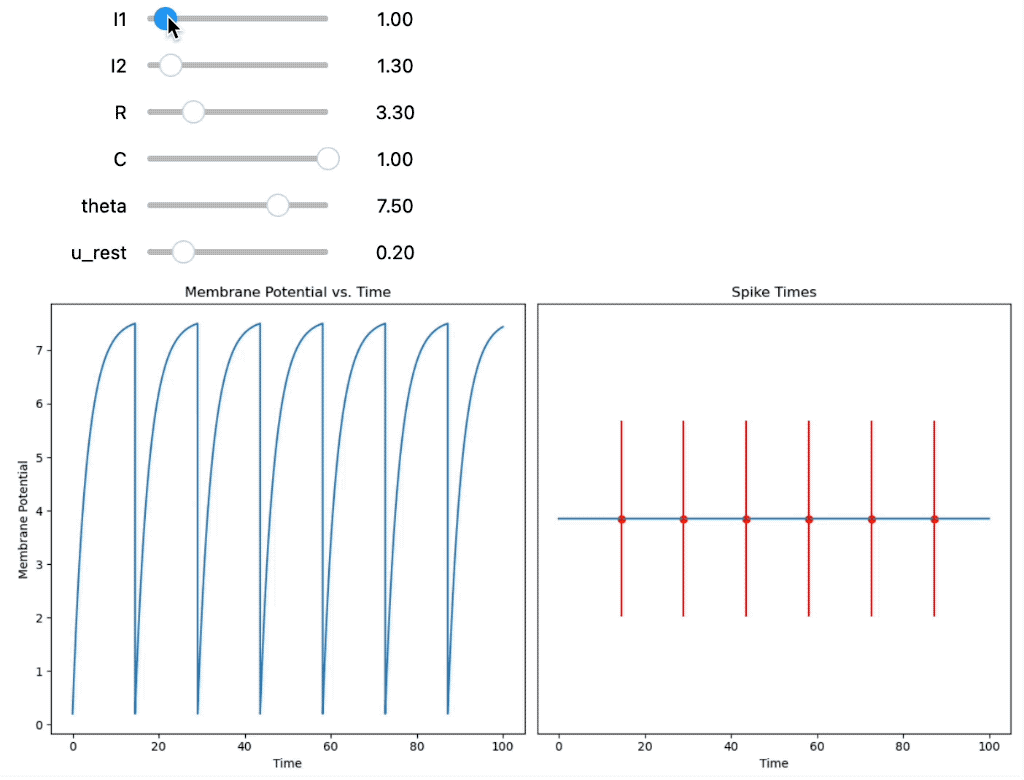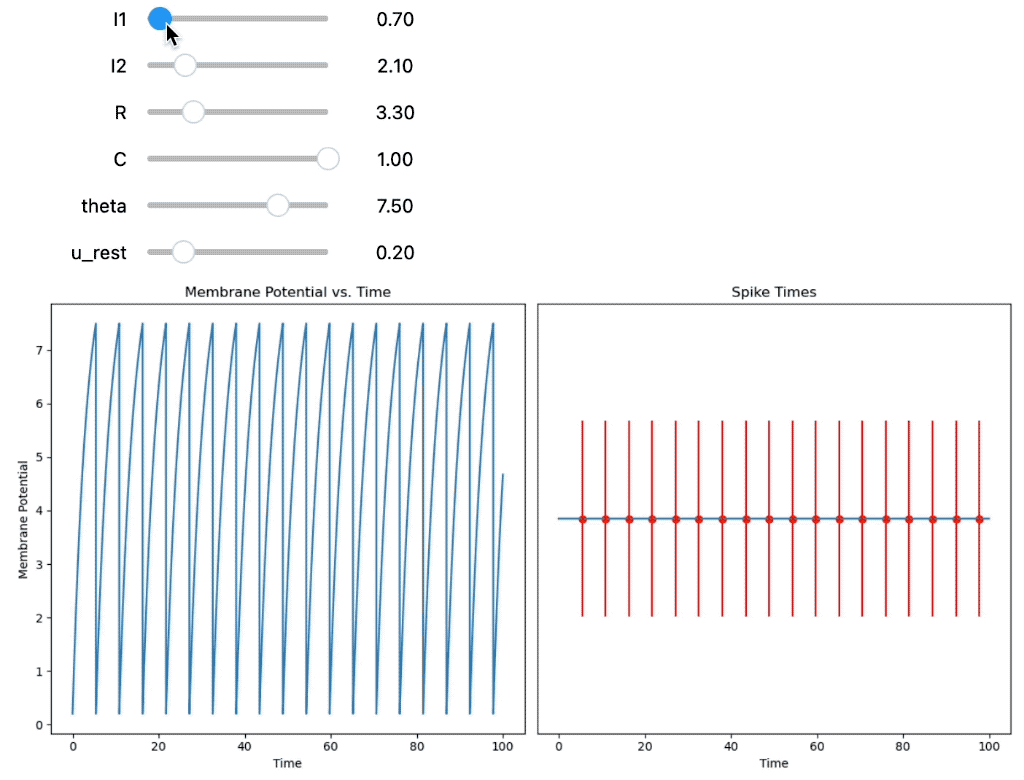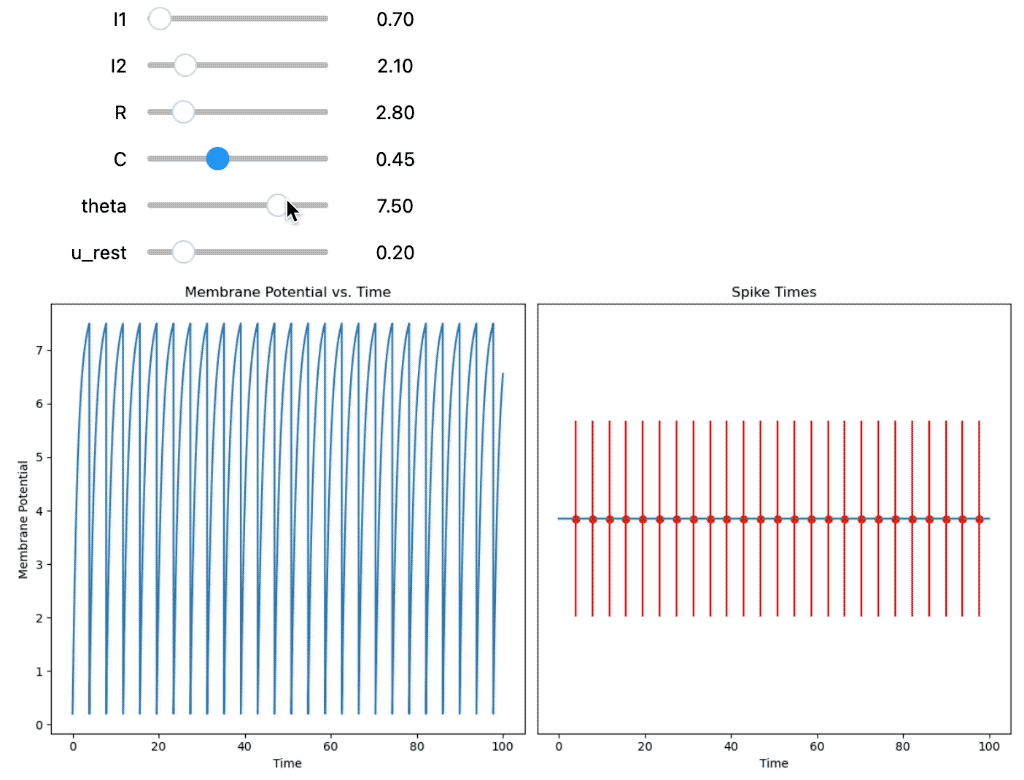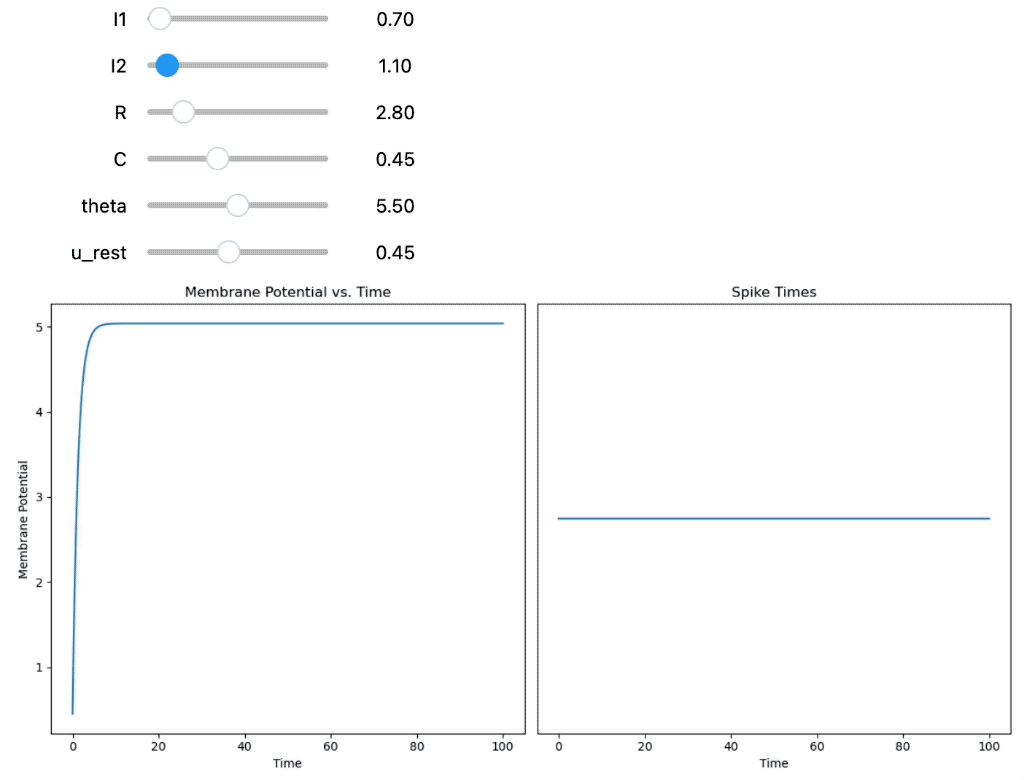Integrate-and-Fire neuron using two constant, but adjustable input currents.

As we can see from the simulations, the input current is not the only factor that determines the neuron’s membrane potential and dynamics. The capacity $C$ and resistance $R$ of the neuron’s membrane also play an important role. The membrane capacity $C$ determines how much charge is needed to change the membrane potential by a certain amount. The membrane resistance $R$ determines how fast the membrane potential changes in response to an input current.

Furthermore, the membrane potential also “leaks” over time due to the resistance of the neuron’s membrane. This leak causes the membrane potential to decay towards its resting state whenever the input current is low or absent. So, even if a large current input is applied to the neuron, if it is not sustained over a sufficient period of time, the neuron may not fire an action potential because the input current may decay before reaching the firing threshold. Conversely, a sustained, lower-intensity current that is applied over a longer period of time may be able to trigger an action potential. Therefore, both the intensity and the timing of the incoming current are crucial for the neuron to reach the firing threshold and generate an action potential in the Integrate-and-Fire model. To demonstrates this, the provided Jupyter notebook also provides a comparison of the following four scenarios:

1. A high intensity current input that decays quickly.
2. A sustained, lower-intensity current.
3. A high intensity current input with long duration.
4. A lower-intensity current input with short duration.

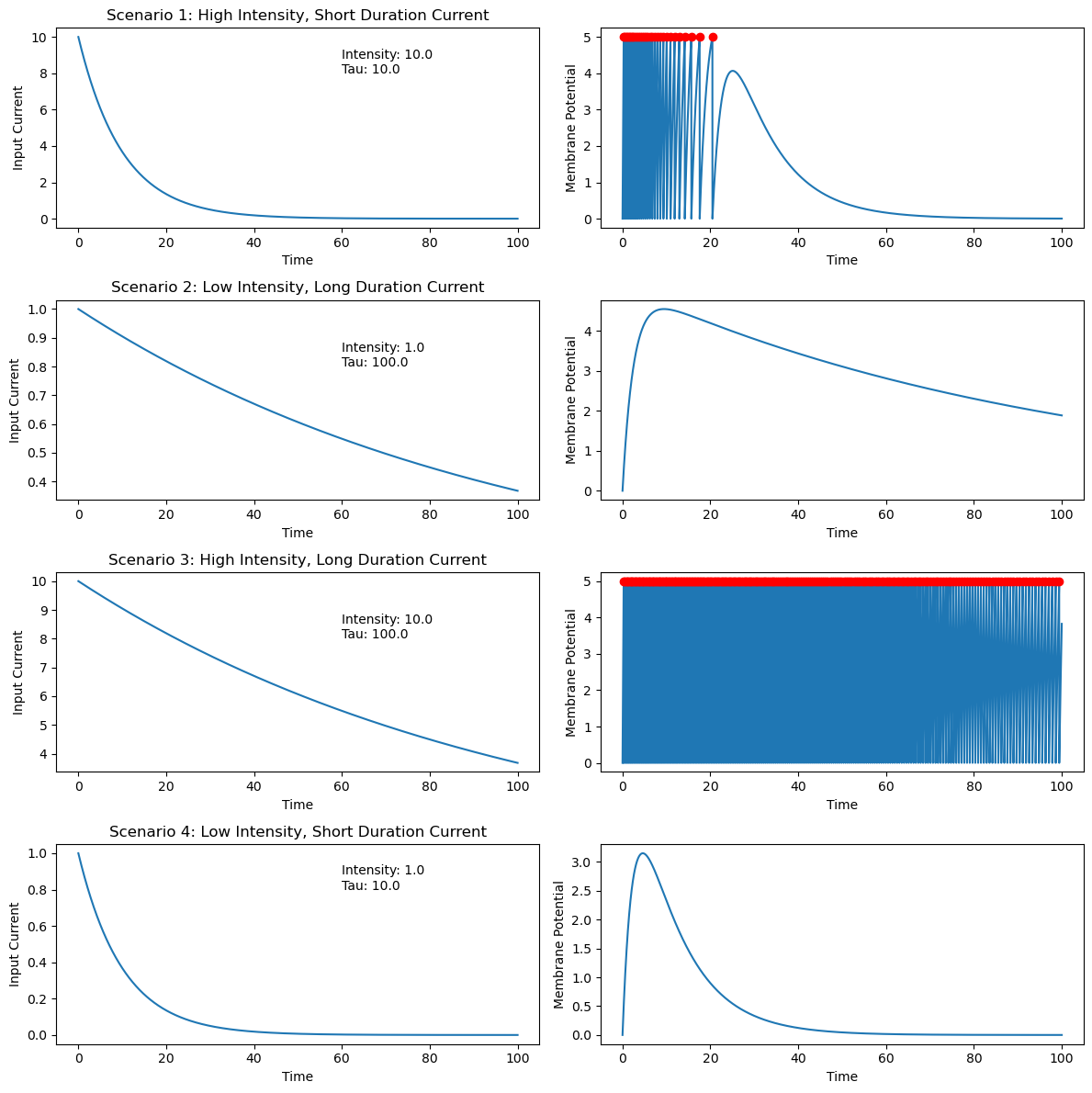Simulating input currents with different intensities and durations.

We see, how quickly the membrane potential decays in the first scenario, even though the input current is much higher than in the second scenario. Using a higher membrane time constant in the third scenario, the membrane potential does not decay over the simulated time period. In scenario two and four, the current intensity was not high enough to reach the firing threshold. However, in scenario two, the current was sustained over a longer period of time.

Please feel free to use the code for your own projects. If you find a bug or have a suggestion for improvement, please open an issue, send me an email or leave a comment in the comment section below.

Comparison with the Hodgkin-Huxley model

The Integrate-and-Fire model and the Hodgkin-Huxley model are two different mathematical frameworks for modeling neurons. Each has its advantages and disadvantages, and their utility depends on the specific requirements of the problem at hand.

Advantages of the Integrate-and-Fire model in comparison to the Hodgkin-Huxley model:

• Simplicity: The Integrate-and-Fire model is mathematically simple and computationally efficient. It is easier to implement and requires less computational resources compared to the Hodgkin-Huxley model.
• Interpretability: The Integrate-and-Fire model has fewer parameters than the Hodgkin-Huxley model, which can make it easier to interpret the effects of these parameters on the model’s behavior.
• Scalability: Because of its simplicity and efficiency, the Integrate-and-Fire model can be used to simulate large networks of neurons, which would be computationally infeasible with more complex models like the Hodgkin-Huxley model.

Disadvantages of the Integrate-and-Fire model in comparison to the Hodgkin-Huxley model:

• Simplicity: The simplicity of the Integrate-and-Fire model is also a disadvantage when it comes to capturing the complex dynamics of real neurons. The model does not account for various biological details, such as the different types of ion channels and their dynamics.
• Accuracy: Because it omits certain biological details, the Integrate-and-Fire model may not accurately predict the behavior of real neurons under certain conditions.

Spiking Neural Networks

Integrate-and-Fire neurons are used in artificial neuronal networks (often referred to as Spiking Neural Networks, or SNNs) to simulate the behavior of biological neurons. These networks attempt to model the dynamics of biological systems more closely than traditional Artificial Neural Networks (ANNs), which use different, simpler models for their neurons.

Here are some reasons why Integrate-and-Fire neurons are useful in SNNs:

• Temporal Dynamics: Integrate-and-fire neurons capture the temporal dynamics of real neurons. In a SNN, the timing of the spikes can carry information, which is a feature not present in traditional ANNs.
• Efficiency: Spiking neurons only need to transmit information when they spike, as opposed to continuously. This makes them potentially more efficient, both computationally and energetically, than traditional ANNs, where every neuron produces an output for every input.
• Biologically Inspired: Because Integrate-and-Fire neurons are a simple model of real neurons, networks that use them can potentially capture more biological phenomena than traditional ANNs. This can be useful in computational neuroscience, where the goal is to understand how real brains compute.
• Learning Rules: There are learning rules like spike-timing-dependent plasticity (STDP) that are naturally defined on the spikes that Integrate-and-Fire neurons produce. These learning rules can be used to train SNNs to perform tasks, and they are often more biologically plausible than the learning rules used in traditional ANNs.

However, there are also challenges associated with using Integrate-and-Fire neurons in artificial networks. For instance, training SNNs can be more difficult than training traditional ANNs, due to the non-differentiable nature of the spiking nonlinearity. Furthermore, while they are a closer model of biological neurons than the units used in ANNs, Integrate-and-Fire neurons are still a simplification, and there are many biological phenomena that they do not capture.

Conclusion

The name “Integrate-and-Fire” comes from how the model processes signals. The neuron “integrates” incoming signals, or in other words, sums up the incoming current over time. When the sum (which corresponds to the membrane potential) crosses a specific threshold, the neuron “fires”, i.e., it generates an action potential and resets its membrane potential.

The beauty of the Integrate-and-Fire model is in its simplicity. Despite being a simplification of the biological processes happening in a real neuron, it captures the essential characteristics of neuronal dynamics: the integration of inputs and the generation of action potentials. The Integrate-and-Fire model is a cornerstone in computational neuroscience, forming the basis for more complex neuron models and large-scale simulations of neural networks.

Please note, that the leaky Integrate-and-Fire model presented here is just one of many variants of the Integrate-and-Fire model. There are many other variants, such as the quadratic Integrate-and-Fire model, the exponential Integrate-and-Fire model, the adaptive Integrate-and-Fire model, and many more. Each of these variants has its own complexity, advantages and disadvantages, and the choice of which model to use depends on the specific research question.

References

The theoretical background of this tutorial is based on the book “Neuronal Dynamics – From single neurons to networks and models of cognition” by Wulfram Gerstner, Werner M. Kistler, Richard Naud and Liam Paninski (Cambridge University Press, 2014), where you can delve deeper into the topic. The book is freely available online at neuronaldynamics.epfl.chꜛ.