New teaching material: Dimensionality reduction in neuroscience

We just completed a new two-day course on Dimensionality Reduction in Neuroscience, and the full teaching material is now freely available under a Creative Commons Attribution 4.0 (CC BY 4.0) license. This course is designed to provide an introductory overview of the application of dimensionality reduction techniques for neuroscientists and data scientists alike, focusing on how to handle the increasingly high-dimensional datasets generated by modern neuroscience research.

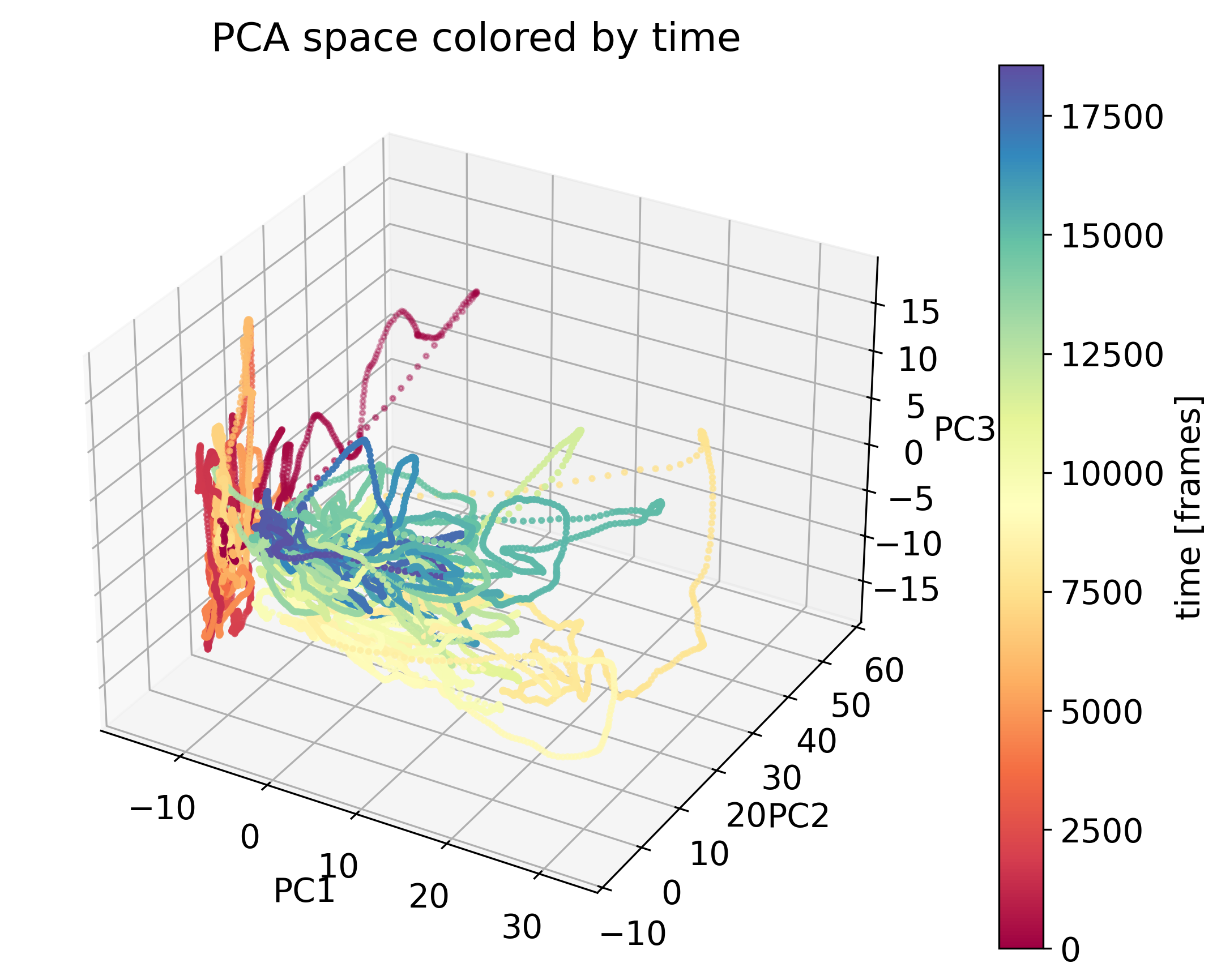
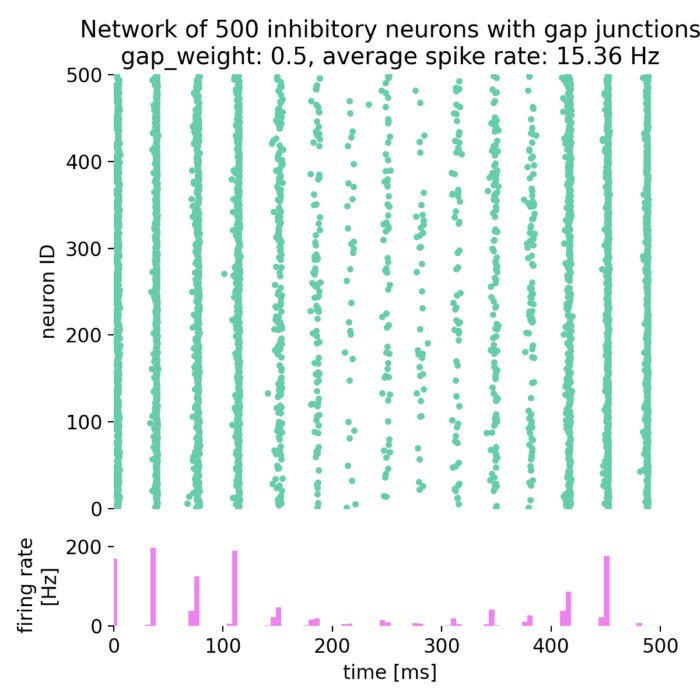
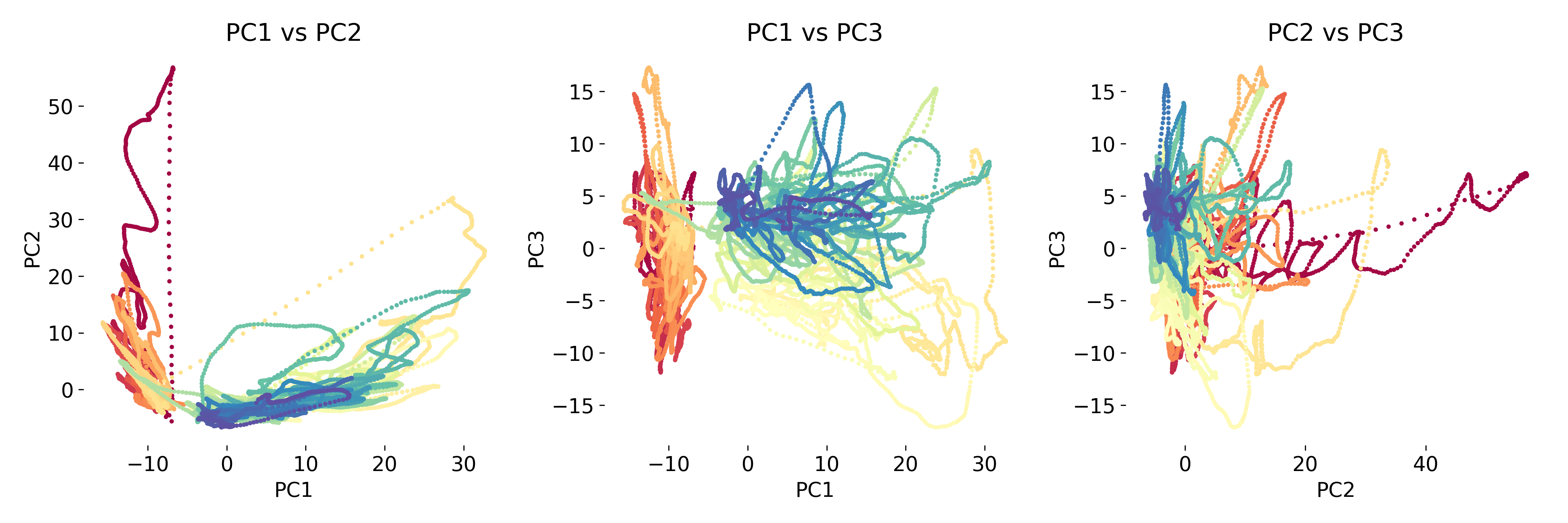PCA of neural data color-coded by time. The data is projected onto the first two principal components, revealing a time-dependent structure. Source of the dataset: ‘Data analysis techniques in neuroscience course 2023ꜛ’ by the Chen Institute for Neuroscience at Caltech / Remedios et al. 2017 (doi: 10.1038/nature23885)ꜛ.

The growing challenge of high-dimensional data in neuroscience

As neuroscience continues to advance, the scale and complexity of the data we collect have increased dramatically. Today, it is common to collect multi-modal datasets that combine:

• Neural recordings (electrophysiology, two-photon calcium imaging, fMRI) from hundreds to thousands of neurons,
• Behavioral data (videos, audio, sensor inputs) collected during experiments,
• Genetic data (RNA sequencing, scRNASeq) that track gene expression at single-cell resolution.

These datasets are often vast, encompassing thousands of dimensions, making them difficult to interpret using traditional analysis methods. The complexity of such data can obscure the underlying patterns that are crucial for understanding brain function and behavior. The primary goal of dimensionality reduction is to transform this high-dimensional data into a more manageable, lower-dimensional form, while retaining the essential structures and patterns. This process makes the data easier to visualize, analyze, and interpret.

What is dimensionality reduction, and why does it matter?

Dimensionality reduction is a set of mathematical techniques that distill the most important information from a high-dimensional dataset into a lower-dimensional representation. This is crucial in neuroscience for several reasons:

• Visualization: High-dimensional data is often impossible to visualize. Dimensionality reduction methods like Principal Component Analysis (PCA) or t-distributed Stochastic Neighbor Embedding (t-SNE) allow researchers to project complex datasets into two- or three-dimensional spaces where they can be visually inspected.
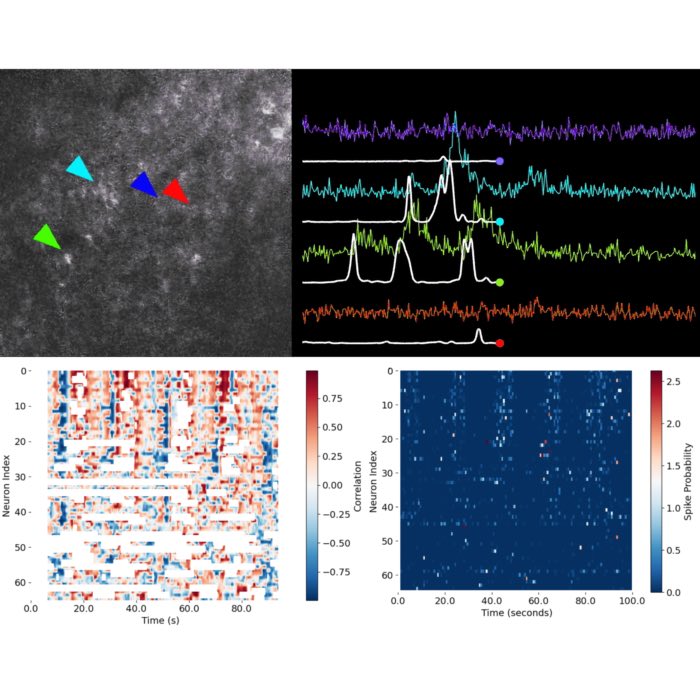
• Identifying patterns: In multi-neuron recordings, for example, dimensionality reduction can reveal population-level dynamics or latent neural states that are not immediately apparent in raw data.
• Noise reduction: High-dimensional data often includes redundant or irrelevant features. Dimensionality reduction helps eliminate noise, allowing researchers to focus on the most meaningful aspects of the data.
• Clustering: By reducing the dimensionality of the data, methods like UMAP and clustering algorithms (e.g., k-means, DBSCAN) can be employed to identify subpopulations of neurons, cells, or behavioral patterns more effectively.

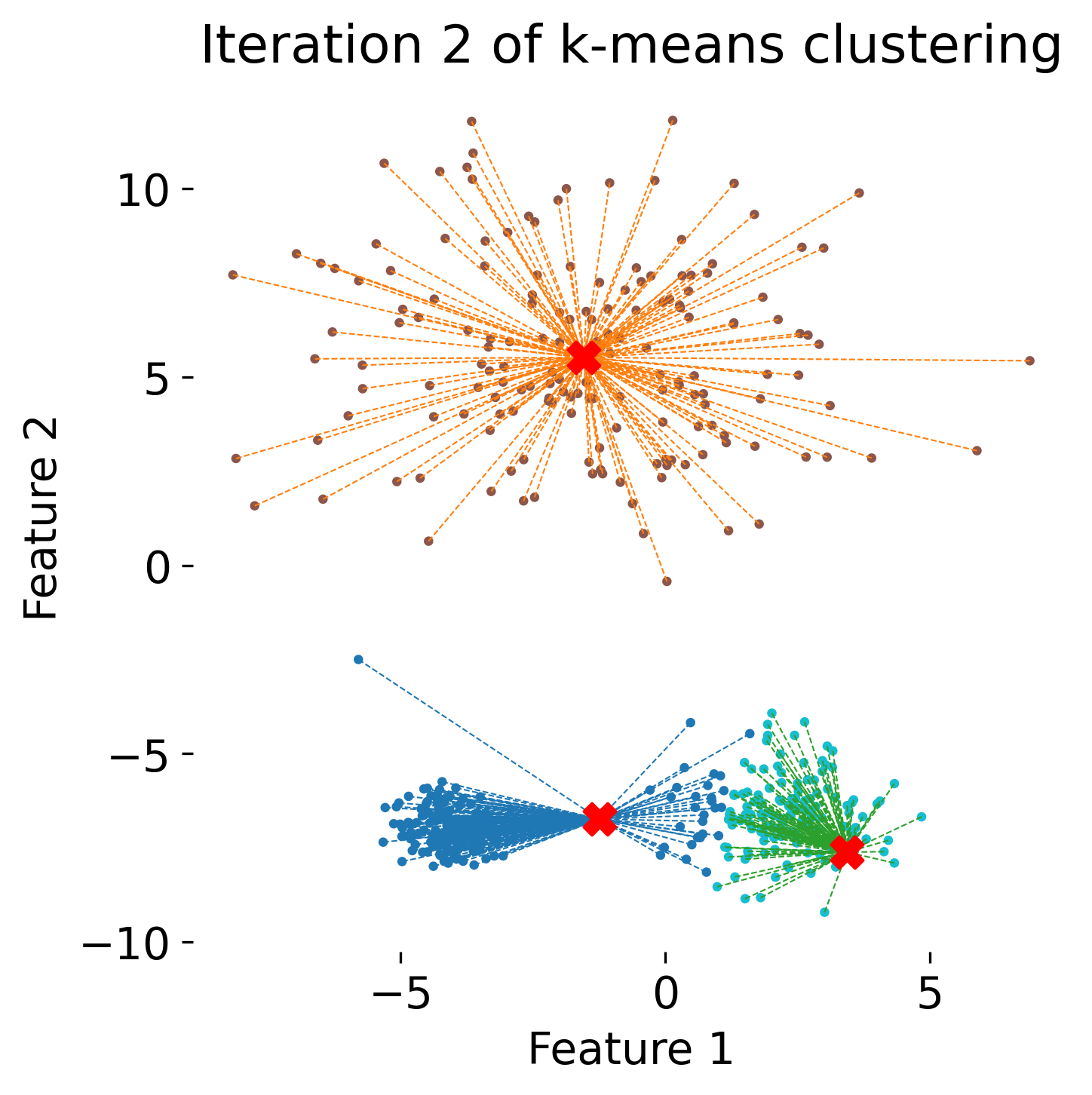Learn how kmeans clustering works.

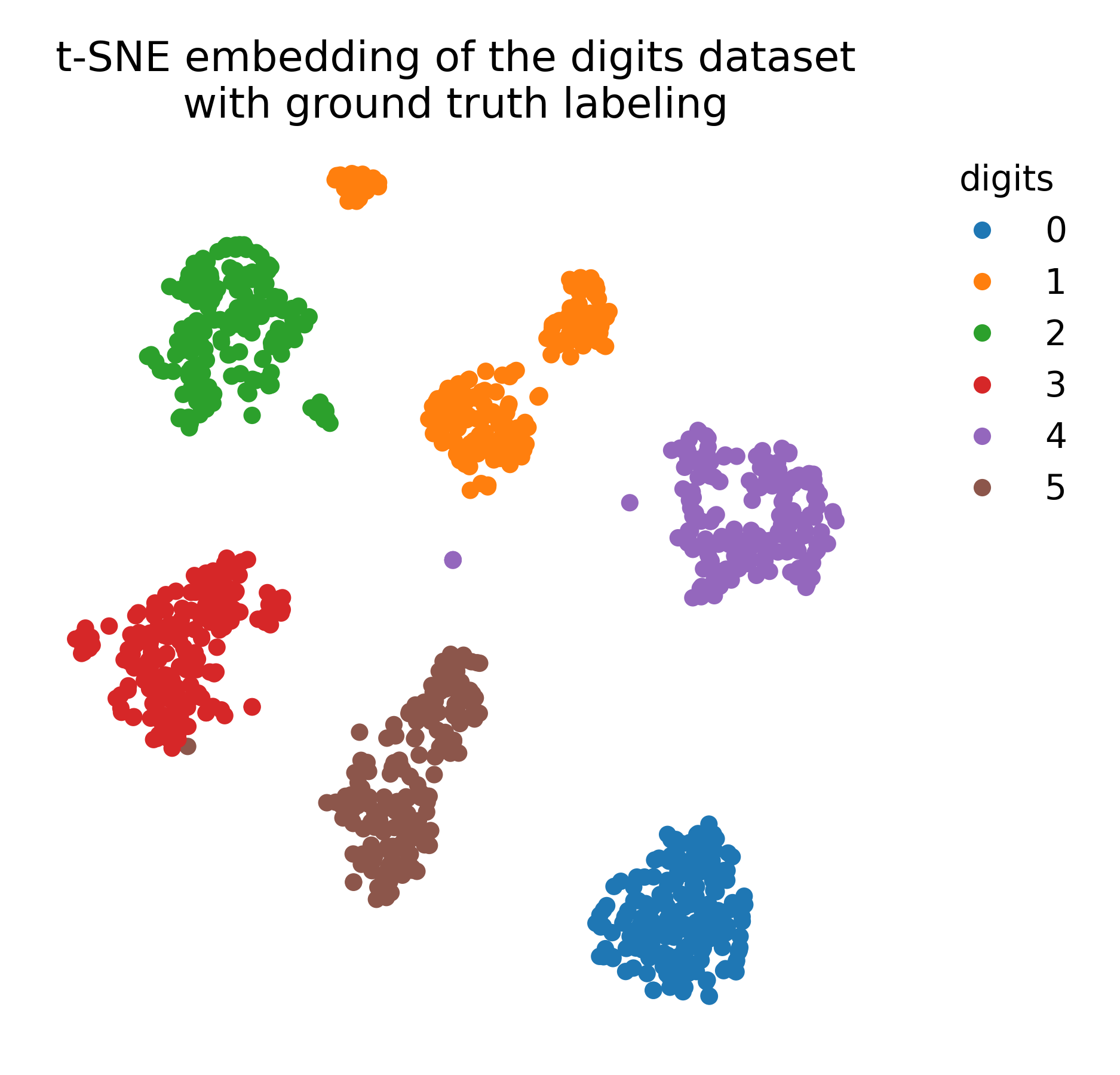
Embedding of the MNIST dataset (left) using t-SNE (right). The t-SNE algorithm reveals the underlying structure of the data, grouping similar digits together.

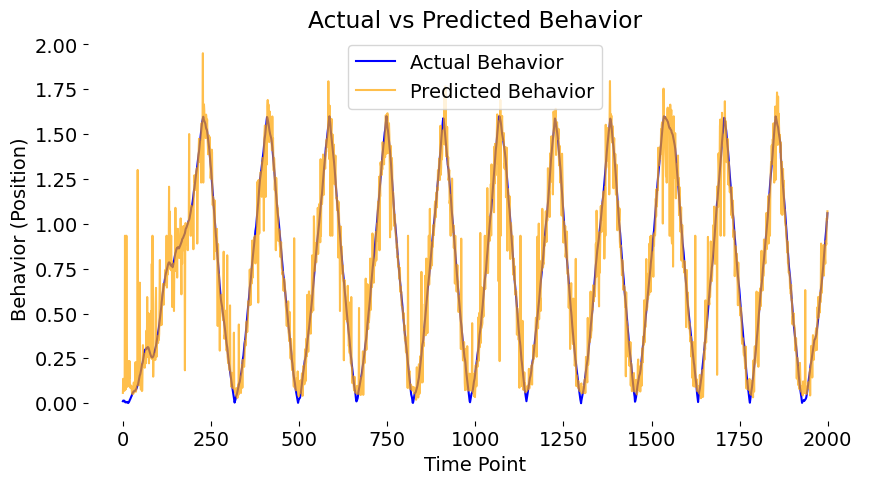Predicting a behavior response by inputting neural data into a a trained autoencoder. The autoencoder learns a compact representation of the neural data that can be used to predict the behavior.

Course content and learning objectives

The course material offers both a theoretical foundation and hands-on practical experience with the most commonly used dimensionality reduction techniques in neuroscience, including:

• Principal Component Analysis (PCA): A linear method that simplifies data by projecting it onto principal components that capture the greatest variance.
• t-SNE (t-distributed Stochastic Neighbor Embedding): A non-linear technique ideal for visualizing high-dimensional data in low-dimensional spaces, often used to explore scRNASeq data and neural population activity.
• UMAP (Uniform Manifold Approximation and Projection): Another non-linear method that improves on t-SNE by preserving both local and global data structures, making it an excellent tool for large datasets.
• Clustering: Techniques such as k-means and DBSCAN for grouping similar data points, which can help identify neural states or cell types based on reduced data.
• Autoencoders: A type of neural network that learns compact, latent representations of data, particularly useful for uncovering hidden factors in large datasets.
• Variational Autoencoders (VAE): A more advanced form of autoencoder that learns probabilistic representations of data, allowing for more flexible and interpretable latent spaces.
• Artificial Neural Networks (ANN): Since we are using autoencoders, we will also cover the basics of neural networks, how they work and how they can be tuned to perform well on a given task.

The material also covers the mathematical foundations of these methods, but with a strong emphasis on practical application. The hands-on Python exercises will help to directly apply these techniques to your own datasets.

Who is this course for?

This course is designed for a wide range of audiences:

• Neuroscientists who are grappling with the analysis of complex, high-dimensional neural data and wish to leverage modern machine learning techniques to uncover hidden patterns.
• Data scientists who are looking to apply their expertise to the field of neuroscience and work with biological datasets.
• Graduate students and researchers in related fields who need a practical introduction to dimensionality reduction techniques, as applied to neuroscience.

A basic understanding of Python programming is recommended, and some familiarity with machine learning concepts will be helpful, but not required. All material is designed to be approachable, with detailed walkthroughs of code examples and exercises.

Course structure and hands-on learning

The course is structured to balance theoretical lectures with hands-on practice. Both, the theoretical part and the hands-on material are designed in such a way, that they can be easily studied without the need to attend the course. The material is self-contained and can be used as a reference for future projects.

Access the teaching material

You can access all of the teaching material, including lecture slides, code notebooks, and sample datasets, here and on this my GitHub repositoryꜛ. The material is released under a CC BY 4.0 license, which means you are free to use, modify, and share it.

Feel free to explore the material and experiment with the provided code. If you have any questions or feedback, please don’t hesitate to reach out. I hope it will help you unlock the potential of your own high-dimensional data and inspires to further explore dimensionality reduction techniques in neuroscience and beyond.