What are alpha-shaped post-synaptic currents?
In some recent posts, we have applied a specific type of integrate-and-fire neuron model, the iaf_psc_alphaꜛ model implemented in the NEST simulator, to simulate the behavior of a single neuron or a population of neurons connected in a network. iaf_psc_alpha stands for “integrate-and-fire neuron with post-synaptic current shaped as an alpha function”. But what does ‘alpha-shaped current’ actually mean? In this short tutorial, we will explore the concept behind it.
General description
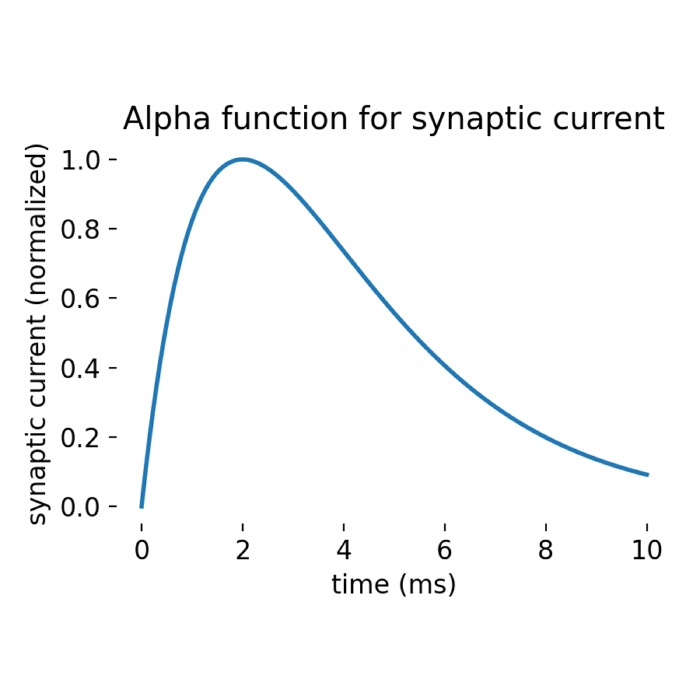
In the context of neural modeling, alpha-shaped post-synaptic currents refer to the specific time course of the synaptic conductance change following a presynaptic spike. This time course is characterized by a rapid rise to a peak value, followed by a slower exponential decay. The mathematical form of this conductance change is given by the alpha function, which describes how the synaptic current evolves over time after a spike. The alpha function is often chosen over other functions such as a simple step function or more complex biophysical models due to its simplicity and computational efficiency, while still capturing the essential dynamics of synaptic transmission.
Alpha Function
The alpha function $\alpha(t)$ is defined as:
\[\alpha(t) = \begin{cases} \frac{t}{\tau} e^{1 - t/\tau}, & \text{for } t > 0 \\ 0, & \text{for } t \leq 0 \end{cases}\]Here, $\tau$ is a time constant that determines the time scale of the rise and decay of the synaptic current.
The alpha function has the following three characteristics:
- rise phase: for $t$ close to zero, the function $\frac{t}{\tau}$ dominates, causing the synaptic current to increase linearly with time.
- peak value: the peak of the alpha function occurs at $t=\tau$, where the current reaches its maximum value $e^{1} / \tau$.
- decay phase: for larger $t$, the exponential term $e^{-t/\tau}$ becomes significant, leading to an exponential decay of the current.
Mathematical formulation of synaptic current
The synaptic current $I_{\text{syn}}(t)$ due to a spike at time $t_j$ from a presynaptic neuron can be expressed using the alpha function as follows:
\[I_{\text{syn}}(t) = w \cdot \alpha(t - t_j)\]where:
- $w$ is the synaptic weight.
- $t_j$ is the time of the presynaptic spike.
- $\alpha(t - t_j)$ is the alpha function shifted to start at $t_j$.
If there are multiple presynaptic spikes occurring at times $t_j$, the total synaptic current is the sum of the alpha functions for each spike:
\[I_{\text{syn}}(t) = \sum_j w_j \alpha(t - t_j)\]where $w_j$ is the weight of the synapse for the $j$-th presynaptic neuron.
Visual representation
To visualize the alpha function, consider the plot below:
import numpy as np
import matplotlib.pyplot as plt
# set global properties for all plots:
plt.rcParams.update({'font.size': 12})
plt.rcParams["axes.spines.top"] = False
plt.rcParams["axes.spines.bottom"] = False
plt.rcParams["axes.spines.left"] = False
plt.rcParams["axes.spines.right"] = False
def alpha_function(t, tau):
return (t / tau) * np.exp(1 - t / tau) * (t > 0)
t = np.linspace(0, 10, 1000)
tau = 2
alpha = alpha_function(t, tau)
fig=plt.figure(figsize=(4.5,3.5))
plt.plot(t, alpha, lw=2)
plt.title('Alpha function for synaptic current')
plt.xlabel('time (ms)')
plt.ylabel('synaptic current (normalized)')
plt.tight_layout()
plt.show()
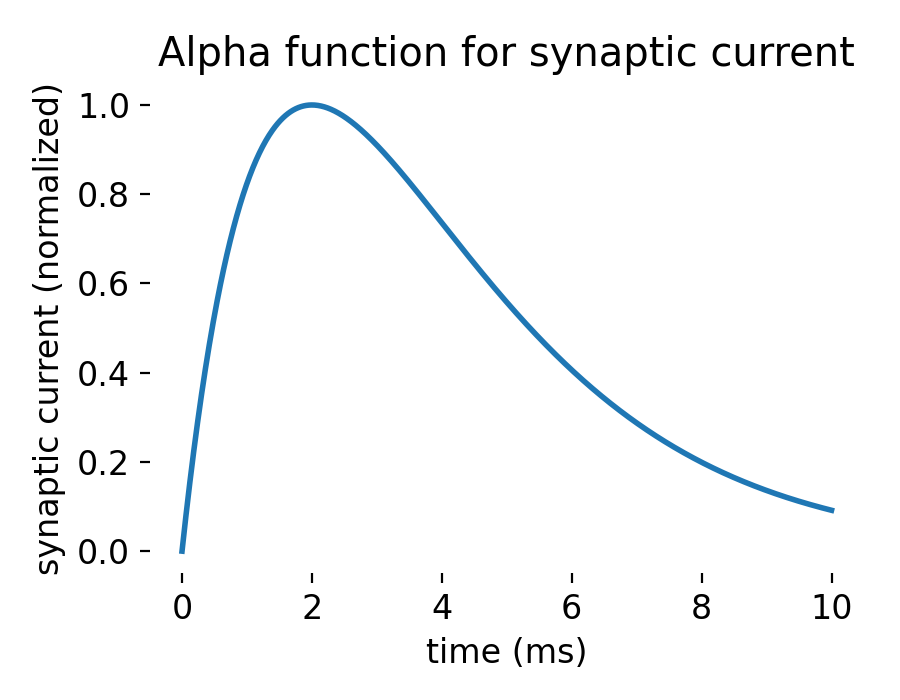
Alpha function for synaptic current. The function rises rapidly to a peak value and then decays exponentially. The time constant $\tau$ determines the shape of the function.
Biological interpretation
The alpha-shaped synaptic current is biologically plausible and commonly used in neural modeling because it captures the essential dynamics of synaptic transmission observed in real neurons. The rapid rise corresponds to the quick response of the postsynaptic neuron to an incoming spike, while the slower decay represents the gradual return to baseline as the neurotransmitter effect dissipates.
Conclusion
In summary, the rise and decay of the synaptic current in an alpha-shaped manner provide a realistic and computationally efficient way to model synaptic interactions in neural networks. This approach is particularly useful in simulations where the timing of spikes plays a crucial role in neural computation. However, it is essential to note that the alpha function is a simplification of the complex dynamics of synaptic transmission, and more detailed models may be required to capture specific aspects of synaptic behavior in different contexts.
The complete code used in this blog post is available in this Github repositoryꜛ (alpha_function.py). Feel free to modify and expand upon it, and share your insights.


comments