Nullclines and fixed points of the Rössler attractor

After introducing phase plane analysis in the previous post, we will now apply this method to the Rössler attractor presented earlier. We will investigate the system’s nullclines and fixed points, and analyze the attractor’s dynamics in the phase space.

Nullclines and fixed points

Let’s recall the system of ordinary differential equations (ODEs) that define the Rössler attractor:

\[\begin{align*} \dot{x} &= -y - z \\ \dot{y} &= x + ay \\ \dot{z} &= b + z(x - c) \end{align*}\]

The nullclines of a system are the curves where the derivative of the variables with respect to time is zero. Thus, to find the nullclines and the fixed points of the system, we start by setting each equation to zero:

\[\begin{align*} \dot{x} =0& \quad \Leftrightarrow \quad y=-z \\ \dot{y} =0& \quad \Leftrightarrow \quad y=-\frac{x}{a} \\ \dot{z} =0& \quad \Leftrightarrow \quad 0 = b + z(x - c) \end{align*}\]

which leads to

\[\begin{align*} y&=-z \\ x&=az \\ 0&= b + z(az - c) = az^2 - cz + b \end{align*}\]

$z$ can be solved for using the quadratic formula:

\[z = \frac{c \pm \sqrt{-4ab + c^2}}{2a}\]

These are the $\dot{x}$-, $\dot{y}$-, and $\dot{z}$-nullclines, respectively.

Given $z$, we can now further specify the values of $x$ and $y$:

\[\begin{align*} x_{1,2} &= a\left(\frac{c \pm \sqrt{-4ab + c^2}}{2a}\right) \\ y_{1,2} &= -\left(\frac{c \pm \sqrt{-4ab + c^2}}{2a}\right) \\ z_{1,2} &= \frac{c \pm \sqrt{-4ab + c^2}}{2a} \end{align*}\]

Thus, there are two fixed points, depending on the value of $z$, which in turn depends on the parameters $a$, $b$, and $c$.

One of the fixed points, usually found near the center of the attractor loop, acts as an “organizing center” for the dynamics, especially in parameter regimes where the attractor exhibits chaotic behavior. Trajectories spiral out from this fixed point, loop around in the characteristic shape of the attractor, and then come back close to it, only to be pushed away again. This fixed point can be thought of as being part of the “chaotic sea” where trajectories move in complex, sensitive, and unpredictable paths.

The other fixed point, lying relatively far from the main attractor loop, typically has a different stability property and doesn’t directly influence the visible structure of the attractor in the same way. Thus, in the following, we will focus on the first fixed point, which is often the more interesting one.

These fixed points are valid assuming that the discriminant $(-4ab + c^2)$ under the square root is non-negative, which is necessary for $z$ to have real values. The presence and stability of these fixed points, as well as the overall behavior of the Rössler attractor, depend significantly on the specific values of the parameters $a$, $b$, and $c$.

Eigenvalues and eigenvectors

To derive the eigenvalues and eigenvectors for the centrally located fixed point, we’ll first specify the fixed point’s coordinates and then linearize the system around this point. The Jacobian matrix $J$ of the system is:

\[J = \begin{bmatrix} \frac{\partial \dot{x}}{\partial x} & \frac{\partial \dot{x}}{\partial y} & \frac{\partial \dot{x}}{\partial z} \\ \frac{\partial \dot{y}}{\partial x} & \frac{\partial \dot{y}}{\partial y} & \frac{\partial \dot{y}}{\partial z} \\ \frac{\partial \dot{z}}{\partial x} & \frac{\partial \dot{z}}{\partial y} & \frac{\partial \dot{z}}{\partial z} \end{bmatrix} = \begin{bmatrix} 0 & -1 & -1 \\ 1 & a & 0 \\ z & 0 & x-c \end{bmatrix}\]

To find the eigenvalues $\lambda$, we solve the characteristic equation obtained by setting the determinant of $J - \lambda I$ to zero, where $I$ is the identity matrix:

\[\begin{align*} \text{det}(J - \lambda I) &= 0 \end{align*}\] \[\begin{align*} \Leftrightarrow \, \text{det}\left( \begin{bmatrix} -\lambda & -1 & -1 \\ 1 & a-\lambda & 0 \\ z & 0 & x-c-\lambda \end{bmatrix} \right) &= 0 \end{align*}\]

By expanding this determinant and simplifying it we obtain the characteristic polynomial of $J$, which is a cubic equation in terms of $\lambda$:

\[-\lambda^3 + \lambda^2(a+x-c) + \lambda(ac-ax-1-z) +\] \[+ x-c+az = 0\]

The characteristic polynomial captures the behavior of the system around the fixed point in terms of the eigenvalues, which indicate the nature of the fixed point (stable, unstable, saddle point, etc.). Inserting the centrally located fixed point’s coordinates and Rössler’s original parameters, $a=0.2$, $b=0.2$, and $c=5.7$, we can solve for the eigenvalues $\lambda$:

\[\begin{align*} \lambda_{1}&=0.0971028+0.995786i \\ \lambda_{2}&=0.0971028-0.995786i \\ \lambda_{3}&=-5.68718 \end{align*}\]

The positive eigenvalues indicate repulsion along the corresponding eigenvector, while the negative eigenvalue indicates attraction. The eigenvectors corresponding to these eigenvalues can be calculated by solving the eigenvalue equation:

\[(J - \lambda I) \mathbf{v} = 0,\]

which leads to:

\[\begin{align*} v_{1}&={\begin{pmatrix}0.7073\\-0.07278-0.7032i\\0.0042-0.0007i\\\end{pmatrix}} \\ v_{2}&={\begin{pmatrix}0.7073\\0.07278+0.7032i\\0.0042+0.0007i\\\end{pmatrix}} \\ v_{3}&={\begin{pmatrix}0.1682\\-0.0286\\0.9853\\\end{pmatrix}} \end{align*}\]

The eigenvectors indicate the directions of the principal axes of the local dynamics around the examined central located fixed point. The first two eigenvalue/eigenvector pairs ($\lambda_{1}/v_1$ and $\lambda_{2}/v_2$) account for the consistent outward movement observed in the primary disc of the attractor. The last pair ($\lambda_{3}/v_3$) is responsible for the attraction along an axis that intersects the manifold’s center, explaining the $z$-motion within the attractor. Furthermore, the complex eigenvalues indicate that the fixed point is a spiral sink, which is consistent with the observable attractor’s behavior. The sign of the real part of the eigenvalues indicates the stability of the fixed point in direction of the corresponding eigenvector: a negative real part indicates stability, while a positive real part indicates instability. The single real, negative eigenvalue of $\lambda_{3}$ indicates stability in the direction associated with that eigenvector ($v_{3}$).

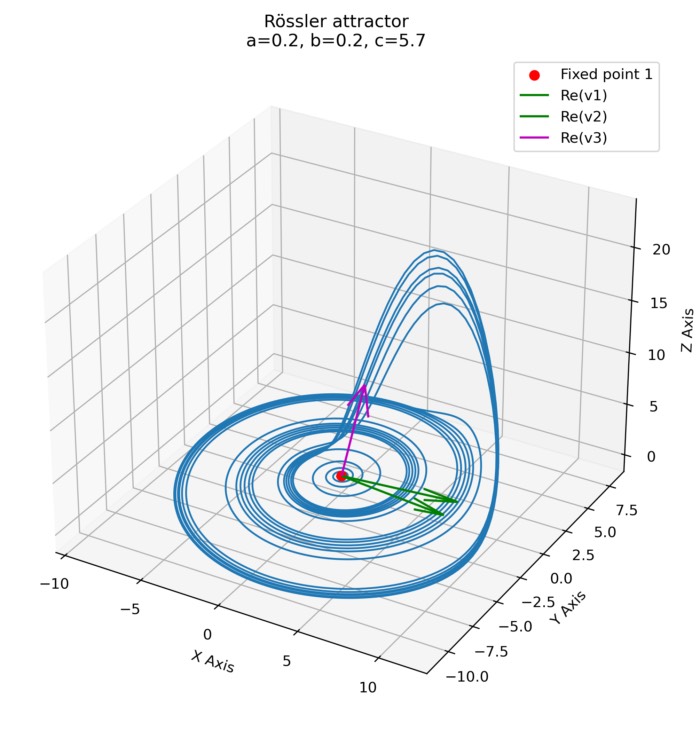
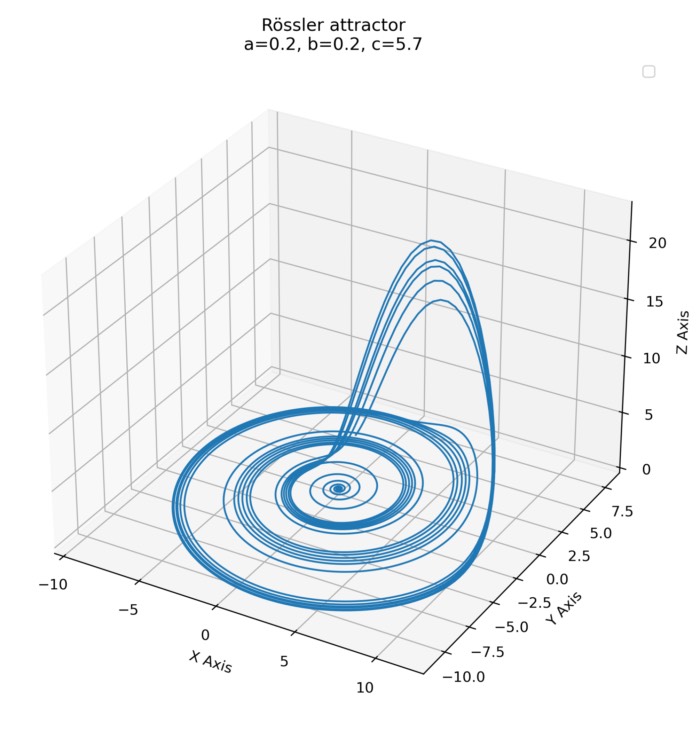
The following plot shows the same plot that we have already generated in the previous post, simulating the attractor using Rössler’s default values ($a = 0.2$, $b = 0.2$, and $c = 5.7$), but with the fixed point and the eigenvectors added:

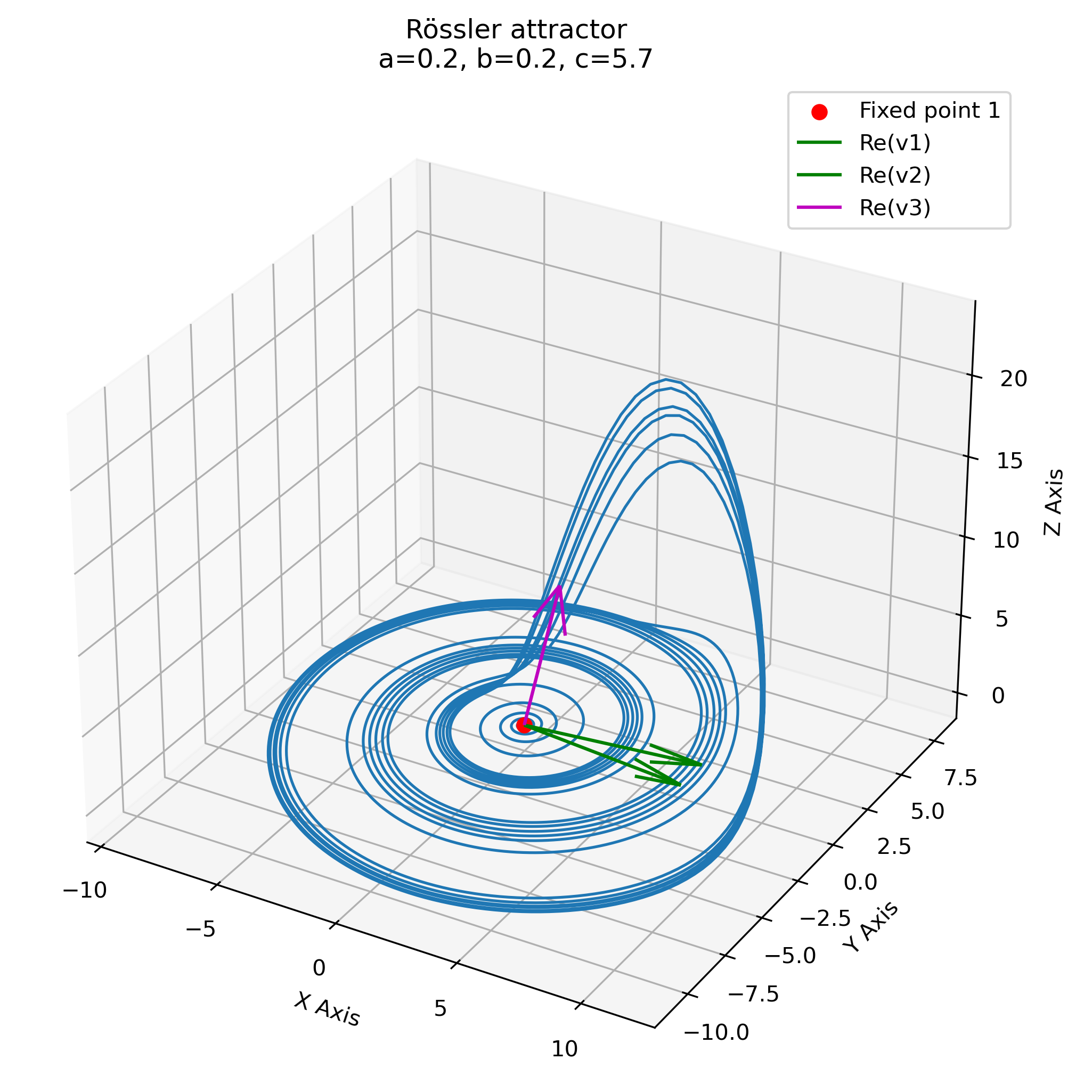The Rössler attractor simulated with parameters $a = 0.2$, $b = 0.2$, and $c = 5.7$. Additionally, the fixed point and the corresponding eigenvectors are shown. The fixed point is marked with a red dot, and the eigenvectors are shown as arrows and indicate the directions of the principal axes of the local dynamics around the fixed point.

The plot is consistent with what we have discussed above. The first two eigenvectors (green vectors) span a plane in which the constant outward movement observed in the primary disc of the attractor occurs (repulsing plane). The third eigenvector (magenta vector) indicates the direction of attraction.

Conclusion

By applying phase plane analysis to the Rössler attractor, we have gained valuable insights into the system’s behavior. We have identified the nullclines and fixed points of the system, and analyzed the attractor’s dynamics in the phase space. We have also calculated the eigenvalues and eigenvectors of the centrally located fixed point, which provide further information about the attractor’s local dynamics. The results are consistent with the observed behavior of the attractor, and we were able to gain a deeper understanding of the system’s structure and behavior.

Overall, we have seen that phase plane analysis is a yet powerful tool to investigate the dynamics of dynamical or chaotic systems, and can provide valuable insights into the systems’ behavior, without the need for extensive numerical simulations.

You can find the code used to generate the plot for this post in this GitHub repositoryꜛ.