Deciphering animal behavior and neuronal activity in latent space (incl. discussion)

6 minute read

↑

In the previous chapters we have seen, that we accumulate vast amounts of data when we record animal behavior and neuronal activity. Behavioral recordings, ranging from extracted motifs from motion-picture footage to more quantifiable metrics such as time-series of animal activity, form a crucial component of this dataset. Another significant element includes recordings of neuronal activity, which often intertwine with behavioral data in intricate ways, thereby mirroring the complexity of the neurological phenomena we seek to understand. These datasets are not merely extensive but also high-dimensional. Each facet of the dataset represents an axis in the high-dimensional space. Moreover, when the data from multiple animals is collated, the size of this dataset multiplies, effectively increasing the dimensions we need to interpret and analyze.

We may therefore ask ourselves: How can we distill meaningful insights and identify patterns, structures, and dynamics that correlate the behaviors with the corresponding neuronal activities? More specifically, how can we identify distinct populations within this high-dimensional data?

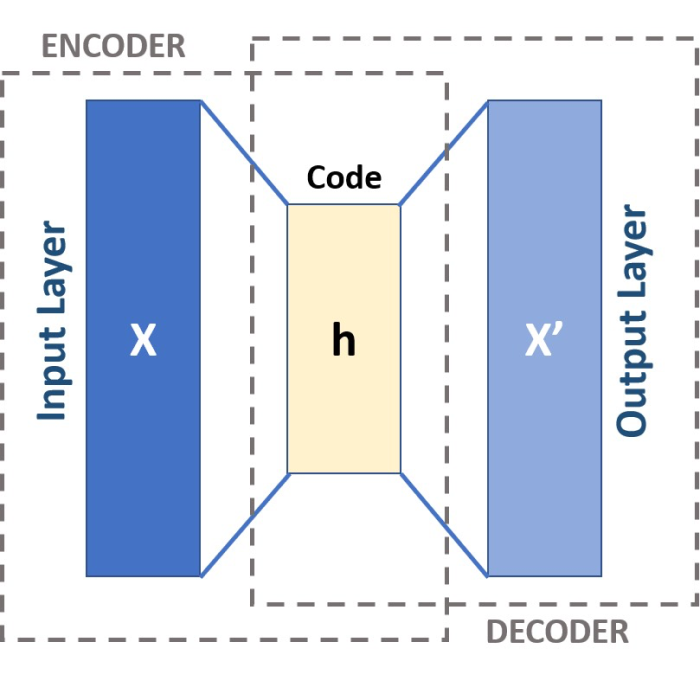
Autoencoders, a type of artificial neural network utilized for learning efficient codings, present a powerful solution to this conundrum. An autoencoder can compress high-dimensional data into a lower-dimensional space, referred to as the coding or latent space. This capability makes autoencoders a suitable tool for tackling our high-dimensional dataset. Within this latent space, the complexity of the original data is encoded into fewer dimensions, making it easier to identify patterns and structures. As a result, this could allow us to discern various populations based on the correlations between behavioral data and neuronal activity.

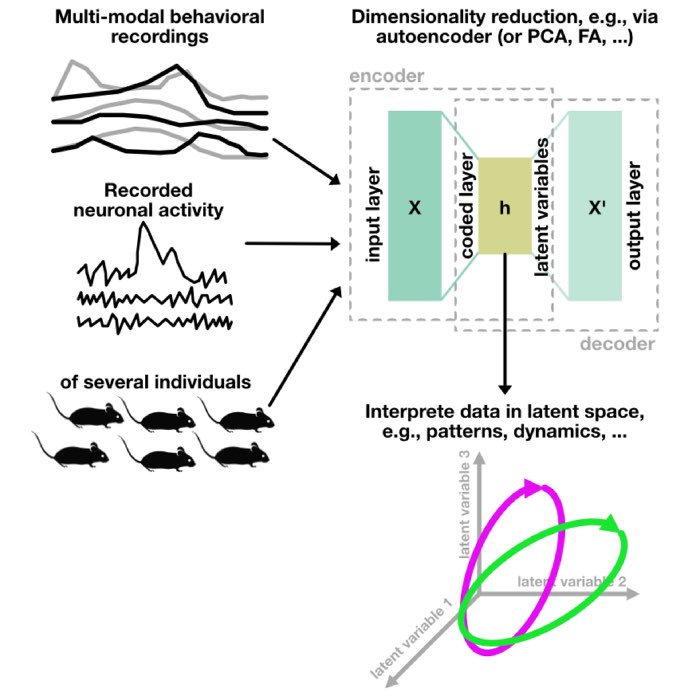
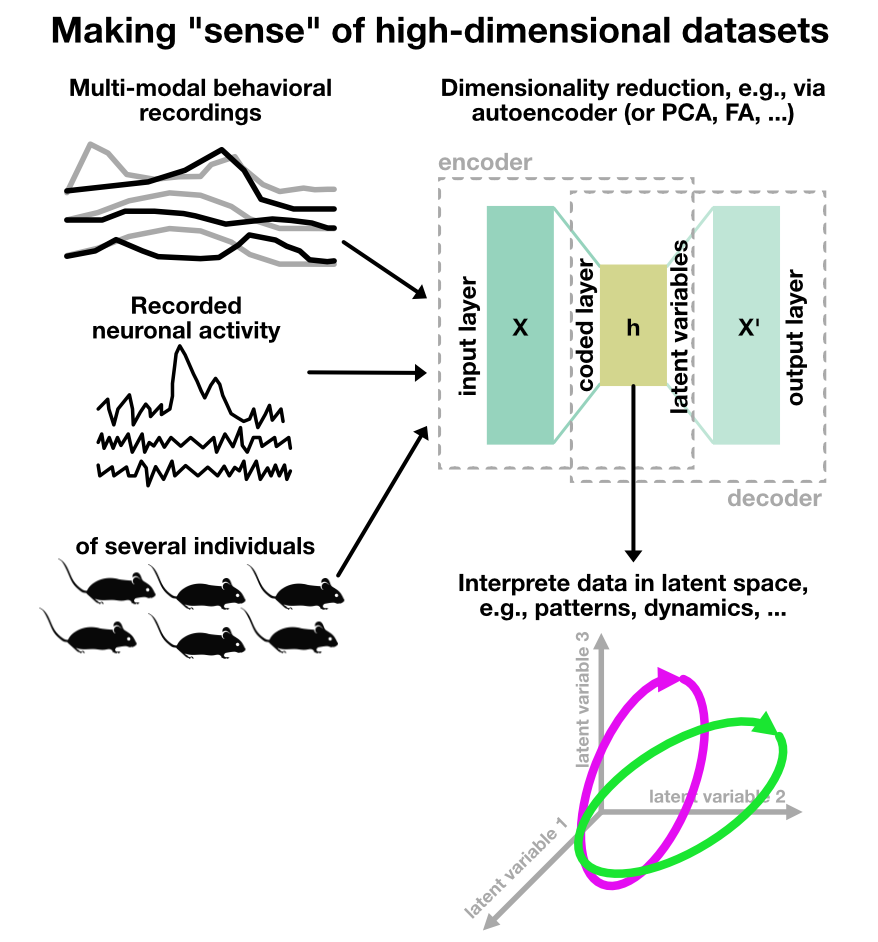png Sketch depicting the use of autoencoders to decipher animal behavior and neuronal activity.

Besides autoencoders, there are many other methods to reduce the dimensionality of high-dimensional data. For example, Principal Component Analysis (PCA) is a popular method to reduce the dimensionality of high-dimensional data. However und unlike autoencoders, PCA is a linear method, which means that it can only capture linear correlations between the data. Another popular method is t-Distributed Stochastic Neighbor Embedding (t-SNE)ꜛ, which is a nonlinear method. However, t-SNE is a non-parametric method, which means that it does not learn a mapping from the high-dimensional data to the low-dimensional space. Instead, it tries to preserve the local structure of the data. This makes it difficult to interpret the resulting low-dimensional space. Autoencoders, on the other hand, are nonlinear and parametric methods. Overall, autoencoders and their variants are one of the most suitable tools for reducing the dimensionality of high-dimensional neuronal and behavioral data.

If you want to see in detail, how autoencoders work and how to program them yourself, check out this blog post. A far more sophisticated and powerful example in this context is CEBRA, which is briefly described in the next section.

If you are interested in Computational Neuroscienceꜛ in general, I highly the book N­euronal Dynamics: From Single N­eurons to Networks and Models of Cognition by Wulfram Gerstner, Werner M. Kistler, Richard Naud, and Liam Paninski. It is a standard and comprehensive textbook in the field and available for free onlineꜛ.

CEBRA

CEBRAꜛ is a newly developed nonlinear dimensionality reduction method that leverages auxiliary behavioral labels and/or time to discover latent features in time series data, specifically in neural recordings. It is designed to address the challenge of explicitly incorporating behavioral and neural data to uncover neural dynamics. CEBRA produces consistent embeddings across subjects, allowing for the identification of common structures in neural activity, and it can uncover meaningful differences and correlations between behavior and neural representations. It combines ideas from nonlinear independent component analysis (ICA) with contrastive learning, a powerful self-supervised learning scheme, to generate low-dimensional embeddings of the data. By training a neural network encoder with a contrastive optimization objective, CEBRA can shape the embedding space and capture the underlying dynamics of neural populations. It has been demonstrated to be highly informative, producing visually interpretable embeddings, and enabling high-performance decoding of behavior from neural activity. CEBRA is applicable to various types of neural data, including calcium imaging and electrophysiology, and it can be used for both hypothesis-driven and discovery-driven analyses. Additionally, it allows for joint training across multiple sessions and animals, facilitating the exploration of animal-invariant features and rapid adaptation to new data.

Here is a collection of links to CEBRA and examples of its application:

Discussion

After reviewing Chapter 1 to 4, let’s discuss the following questions:

  1. Why performing animal behavior experiments?
  2. What do you have to respect when performing animal behavior experiments?
  3. What are three common animal species for performing animal behavior experiments in neuroscience and why?
  4. What is multi-modal behavior phenotyping? What are high-throughput behavioral experiments? Name advantages compared to “traditional” experiments and examples for both approaches. Also, think about potential disadvantages.
  5. What are the three main types of machine learning?
  6. Briefly describe the approach to decipher high-dimensional behavioral and neuronal data. Why is this even necessary?

Further readings

If you want to delve deeper into the topic of this chapter, I recommend the following resources:

  • Wulfram Gerstner, Werner M. Kistler, Richard Naud, and Liam Paninski (2014), Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition, , Cambridge University Press, online versionꜛ
  • R. B. Ebitz, & B. Y. Hayden, The population doctrine in cognitive neuroscience, 2021, Neuron, Vol. 109, Issue 19, pages 3055-3068, url, doi: 10.1016/j.neuron.2021.07.011ꜛ
  • R. Yuste, From the neuron doctrine to neural networks, 2015, Nat Rev Neurosci, Vol. 16, Issue 8, pages 487-497, url, doi: 10.1038/nrn3962ꜛ
  • S. Saxena, & J. P. Cunningham, Towards the neural population doctrine, 2019, Curr Opin Neurobiol, Vol. 55, pages 103-111, url, doi: 10.1016/j.conb.2019.02.002ꜛ
  • John P. Cunningham, & Byron M. Yu, Dimensionality reduction for large-scale neural recordings, 2014, Nat Neurosci, Vol. 17, Issue 11, pages 1500-1509, url, doi: 10.1038/nn.3776ꜛ
  • T. P. Vogels, K. Rajan, & L. F. Abbott, Neural network dynamics, 2005, Annu Rev Neurosci, Vol. 28, pages 357-376, url, doi: 10.1146/annurev.neuro.28.061604.135637ꜛ
  • M. R. Cohen, & J. H. Maunsell, A neuronal population measure of attention predicts behavioral performance on individual trials, 2010, J Neurosci, Vol. 30, Issue 45, pages 15241-15253, url, doi: 10.1523/JNEUROSCI.2171-10.2010ꜛ
  • R. Laje & D. V. Buonomano, Robust timing and motor patterns by taming chaos in recurrent neural networks, 2013, Nat Neurosci, Vol. 16, Issue 7, pages 925-933, url, doi: 10.1038/nn.3405ꜛ
  • David Sussillo, Neural circuits as computational dynamical systems, 2014, Curr Opin Neurobiol, Vol. 25, pages 156-163, url, doi: 10.1016/j.conb.2014.01.008ꜛ
  • Peiran Gao, & Surya Ganguli, On simplicity and complexity in the brave new world of large-scale neuroscience, 2015, Current opinion in neurobiology, url, doi: 10.48550/arXiv.1503.08779ꜛ
  • Juan A. Gallego, Matthew G. Perich, Lee E. Miller, & Sara A. Solla, Neural Manifolds for the Control of Movement, 2017, Neuron, Vol. 94, Issue 5, pages 978-984, url, doi: 10.1016/j.neuron.2017.05.025ꜛ
  • J. D. Murray, A. Bernacchia, N. A. Roy, C. Constantinidis, R. Romo, & X. J. Wang, Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex, 2017, Proc Natl Acad Sci U S A, Vol. 114, Issue 2, pages 394-399, url, doi: 10.1073/pnas.1619449114ꜛ
  • Joao D. Semedo, Amin Zandvakili, Christian K. Machens, Byron M. Yu, & Adam Kohn, Cortical Areas Interact through a Communication Subspace, 2019, Neuron, Vol. 102, Issue 1, pages 249-259.e4, url, doi: 10.1016/j.neuron.2019.01.026ꜛ
  • H. Sohn, D. Narain, N. Meirhaeghe, & M. Jazayeri, Bayesian Computation through Cortical Latent Dynamics, 2019, Neuron, Vol. 103, Issue 5, pages 934-947.e5, url, doi: 10.1016/j.neuron.2019.06.012ꜛ
  • Saurabh Vyas, Matthew D. Golub, David Sussillo, & Krishan V. Shenoy, Computation Through Neural Population Dynamics, 2020, Annu Rev Neurosci, Vol. 43, pages 249-275, url, doi: 10.1146/annurev-neuro-092619-094115ꜛ
  • K. V. Shenoy, & J. C. Kao, Measurement, manipulation and modeling of brain-wide neural population dynamics, 2021, Nat Commun, Vol. 12, Issue 1, pages 633, url, doi: 10.1038/s41467-020-20371-1ꜛ
  • Evren Gokcen, Anna I. Jasper, João D. Semedo, Amin Zandvakili, Adam Kohn, Christian K. Machens, & Byron M. Yu, Disentangling the flow of signals between populations of neurons, 2022, Springer Science and Business Media LLC, Nature Computational Science, Vol. 2, Issue 8, pages 512-525, url, doi: 10.1038/s43588-022-00282-5ꜛ

updated:

3 other articles are linked to this site